過不足算の演習１

過不足算といえばよく出題されるのが「長いすに生徒が座る」問題です．ここでは具体的な問題を見ながら過不足算の演習に取り組んでみましょう

さっそく線分図を描いてみましょう．このとき，「過不足算の解法」で確認したとおり，まずは生徒の長さを先に決めることが重要です．

長いすの数を①として線分図を描いていきましょう．

4人ずつ座ったときは，16人が座れない，つまり，長いすの許容人数に対して16人が余りになります．

5人ずつ座ったときは，まず14脚は完全に空いているので，5×14＝70人がさらに座れます．また，5人に満たない人数が座った長いすが1脚できているのでさらに「1～4人」が座れることになります．つまり，長いすの許容人数に対して70＋1～4人＝71～74人が不足となります．

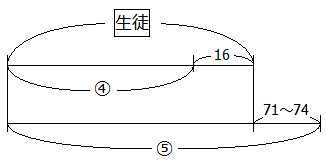
差に注目すると次のように描けます．

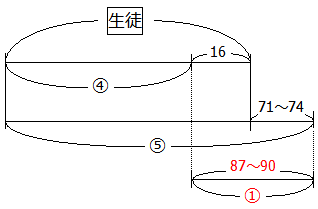
①＝87～90，つまり長いすは87～90脚であることが分かります．

長いすの数がいまいちはっきりしませんが，生徒の数は6の倍数であることが分かっています．ですので，長いすの数が87～90脚の場合についてそれぞれ生徒の人数が何人になるかを計算してみることにします．

【87脚のとき】　4×87＋16＝364人

【88脚のとき】　4×88＋16＝368人

【89脚のとき】　4×89＋16＝372人

【90脚のとき】　4×90＋16＝376人

このうち6の倍数であるのは372なので，生徒の人数は372人（長いすの数は89脚）と求まります．

（6の倍数の見分け方は「倍数の見分け方」も参考にしてください）

この問題を難しくしているポイントは２点あります．

ひとつは『線分図に余りと不足をきちんと表しにくい』ことです．

"長いすの許容人数に対して"余りと不足を考える，という点をよく確認しましょう．（このとき線分図上で「生徒の長さ」を先に決めていなければ余計に混乱してしまいます）

もうひとつは『長いすの数が最後まで決まらない』ことです．

最後に6の倍数になるのはどれかを調べ上げる計算が必要となります．最終的に調べ上げを行って条件に合う答えを見つける，という応用問題は過不足算に限らずよく登場しますので，色々な問題を解いていく中で慣れるようにしましょう．