つるかめ算の基本

つるかめ算は数ある中学受験算数の問題の中でも最も知名度が高い（？）問題です．つるかめ算は面積図の使い方の描き方さえマスターすれば解答が難しい問題ではありませんのでよく確認しておきましょう．

では具体的な問題を見てみましょう．

ではさっそく面積図を描いてみましょう．面積図を描くときのポイントは「合計の個数を横に，それぞれ1個の値段を縦に描く」ことです．この問題の場合，面積図の横が15個，縦が100円，120円となります．そして，合計金額の1600円がこの図の面積になります．

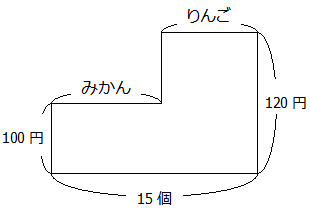
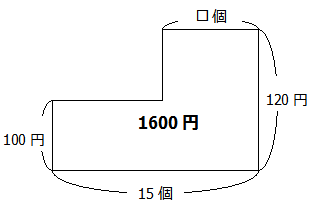
さて，つるかめ算は，消去算と同様，「どちらかに揃える」ことが必要です．ではこの場合はみかんとりんごのどちらに揃えるべきか？・・・もうお気づきでしょうが，この問題では「りんご」の個数が知りたいので「みかん」に揃えればよいのです．

みかんに揃えるということは，面積図から次のように考えることができます．

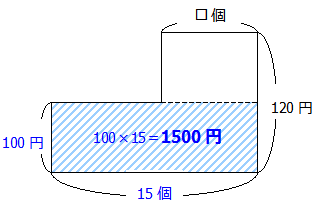
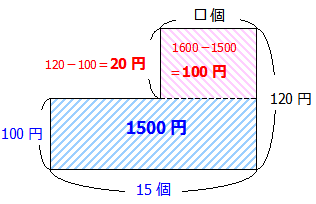
よって□を求めたければ次のように計算します．

100×15＝1500円　（すべてをみかんに揃えたときの値段）

1600－1500＝100円　（実際の金額との差）

120－100＝20円　（りんごとみかんの１個の値段の差）

100÷20＝５個　（りんごの個数）　答：５個

※慣れてくれば，「(1600－1500)÷(120－100)＝５」というように一つの式で書けるようになります．

この問題も考え方は問題1と同じです．

鉛筆を求めたいので「消しゴム」に揃えて考えます．ただし，この場合，問題1とは面積図の使い方が少し異なるので注意しましょう．

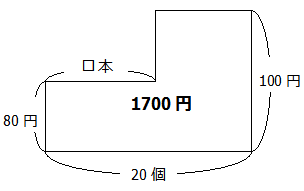
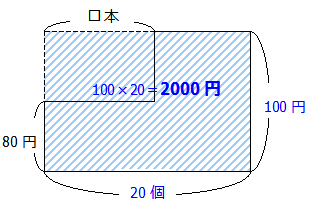
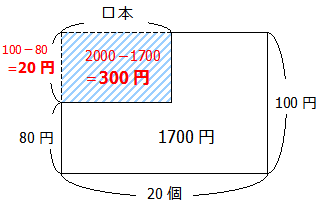
以上より□を求める計算は次のように計算します．

100×20＝2000円　（すべてを消しゴムに揃えたときの値段）

2000－1700＝300円　（実際の金額との差）

100－80＝20円　（消しゴムと鉛筆の１個の値段の差）

300÷20＝15本　（鉛筆の本数）　答：15本

一つの式で書くと「(100×20-1700)÷(100－80)＝15」となります．

つるかめ算を解くときの面積図の描き方は以上２つのパターンがありますので，どちらもしっかりマスターするようにしましょう．

つるかめ算の解法としては，面積図を描かずに「答えを求めなくてもよい方に揃える」ことにより式だけで計算する解説もしばしば見受けられます．しかしそれでは式の操作が何を表しているかを理解することができず，基本的な問題ならまだしも，応用問題となってくると解けなくなる，ということもありますので，つるかめ算を解く際には必ず面積図で考えることを勧めます．

５年生以降ではつるかめ算は面積図で考えるのが基本ですが，低学年（4年生）では次のように表で考えさせることもあります．

[問題1の場合]

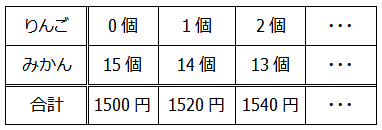
表で考えるのは時間がかかりますが確実に答えにたどり着くことができます．また，このような表の考え方は数列などの規則性の問題の考え方にも通じます．

さて，つるかめ算は，「その問題がつるかめ算だと分かっていれば」解答が難しい問題ではありません．つるかめ算の最も難しいところは「その問題がつるかめ算であることを見抜くこと」にあります．つるかめ算はいつも今回の例題のような単純な形で出題されるとは限りません．平面図形や速さの問題の中に潜んでいることもあります．そのような問題から「こいつはつるかめ算だ！」と子ども自身に気付かせるのは非常に難しいことです．

そういった点からも，普段から問題の様子を図に表して考えるクセをつけておけば，単に式の操作だけで問題を解くよりは何倍も「つるかめ算であること」に気付きやすくなると思います．

様々な分野に登場するつるかめ算の例は以下の通りです．