つるかめとんぼ算　その２

つるかめとんぼ算　その１では面積図に注目して「つるかめ算の基本形」を見つけるという問題を確認しましたが，今回はさらに応用問題を見てみましょう．

さっそく問題です．

ではさっそく面積図を書いてみましょう．

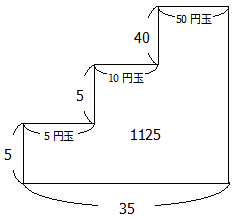
つるかめとんぼ算　その１と同様左上に注目してみましょう．

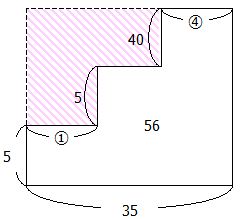
しかし・・・比がわかっているのは5円玉と50円玉であるため，うまく求められません．よって別の方法を考えなくてはなりません．

では，どうすれば3種類の硬貨のつるかめ算を2種類の硬貨のつるかめ算にできるのか？

この場合ちょっと強引ですが「無理やり新しい硬貨を作ればよい」のです．

いま，5円玉と50円玉の数の比がわかっているので新しく「5円玉と50円玉を平均した新硬貨」を作ってみましょう．

といっても，5円玉と50円玉なので平均して(5＋50)÷2＝27.5円玉を作る！というのは早とちりです．（参考：『平均』の計算に注意！）

では，どう考えればよいでしょう・・・？

面積図をよく見てみましょう．

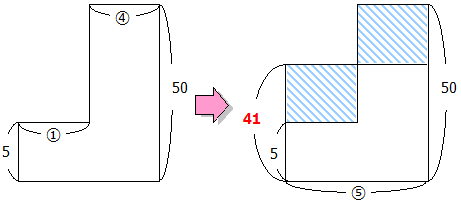
5円玉と50円玉の合計面積は

5×①＋50×④＝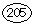

よって平均は

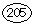÷⑤＝41円となります．

よってこの問題は「10円玉と41円玉が合わせて35枚で合計金額は1125円」と考えることができるのです．

これを面積図で表すと次の通りです．

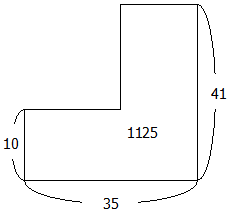
これはもう単純なつるかめ算です．

10円玉，41円玉のどちらから求めてもよいですが，10円玉を求めると，

(35×41－1125)÷(41－10)＝10枚となります．

41円玉は35－10＝25枚となりますが，

⑤＝25枚なので

①＝5枚となります．

よって，5円玉は5×1＝5枚，10円玉は5×4＝20枚と求まるのです．

つるかめとんぼ算にいきなり「平均」の考え方を使うというのは，なかなか思いつかない発想かもしれません．しかし，「平均することで問題が簡単になる」，という場面は実はつるかめ算以外にもあります．

解答に詰まったときは「平均が使えるかも・・・」というように，自分の頭の引き出しから常により多くの発想を取り出せるようにしておくことは受験算数において非常に重要です．

また，平均を求めるときは単純に「足して２で割る」ことのないように注意しましょう．