売買算の演習１

売買に関する問題には値上げしたり値引きしたりと，様々なシチュエーションがありますが，ここでは比較的出題頻度の高い「品物をこわしてしまった」場合の問題と「つるかめ算になる」タイプの問題を取り上げてみたいと思います．

「ある品物」って何・・・？そして「こわすなよ！」と思わず突っ込みたくなるところですが，実社会では十分にあり得ることです．

こういう問題のパターンでは，「もし1個もこわしていなかったら」と考えることが大切です．実社会ではいくら「もしあのときこわしていなかったら・・・」と考えても何の解決にもなりませんが，この問題の場合はそう考えることで解決できてしまいます．

では計算してみましょう．

仕入れ値は1個120円なので利益は1個あたり180－120＝60円です．よって1個もこわさずに売った場合の利益は23460＋60×18＝24540円・・・と計算してしまうとまちがいです！

なぜならば，18個こわしてしまっても，すでに23460円の利益があるということは，この18個分の売り上げはそのまま全額利益に上乗せされるからです．

よって，利益は23460＋180×18＝26700円と計算するのが正解です．

1個あたりの利益は60円なので，この品物の個数は26700÷60＝445個となります．

つるかめ算は売買の問題にも潜んでいることがあります．次の問題を見てみましょう．

全体の売り上げと個数が分かっていて，求めるのは片方の個数・・・典型的なつるかめ算です．

つるかめ算の基本でも強調していますが，つるかめ算は問題文をいくら読んでもそこに「この問題はつるかめ算ですよ」とは書いていません．つるかめ算のポイントは「その問題がつるかめ算であることを見抜くこと」にあります．

つるかめ算とわかってしまえばあとは面積図を描けば解けるはずです．

まず，定価の15％引きを計算しておきましょう．

4800×(1－0.15)＝4080円

これで面積図を描く材料はそろいました．

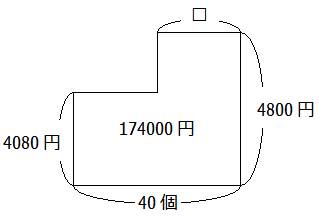
各量が面積図の縦になるのか横になるのか面積になるのかに不安がある場合は，つるかめ算の基本で確認してみてください．

あとは計算するだけです．求めたいのは定価で売れた個数（図中の□にあたる個数）なので，すべてを「15％引き」にそろえる，という方向で計算を進めます．

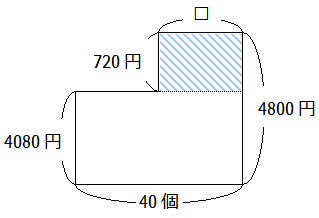
4080×40＝163200円

174000－163200＝10800円（図の斜線部分）

4800－4080＝720円（斜線部の縦）

10800÷720＝15個（求める□の個数）

となります．