数列の基本
ただでさえ苦手とされやすい算数の中でも「数列」は特に苦手とされやすい分野のひとつです.数が少ないうちは力技でなんとか答えまでたどり着くこともできますが,数が多くなってくるとそうはいきません.
数列分野では「規則性」の把握とその運用の仕方が重要となります.ここではまずそんな数列の基本的事項をおさらいしておきましょう.
等差数列の公式は覚えてしまおう
数列の問題で出題率が高いのは,一定の数ずつ増えてゆく「等差数列」です.等差数列では『□番目の数』の求め方と,『和』の求め方を暗記しておく必要があります.
まず等差数列の『□番目の数』ですが,公式は次の通りです.
・『□番目の数』=初項+公差×(□-1)
具体的な等差数列を見てみましょう.
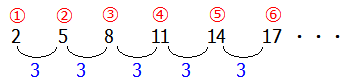
『初項』とは「最初の数」のことです.この数列だと初項は『2』です.
『公差』とは並んでいる数と数の差のことです.この数列だと公差は『3』で常に一定です.
具体的に上の公式にあてはめてこの数列の6番目の数を計算してみると,
『6番目の数』=2+3×(6-1)=17
となります.たしかに6番目の数は17になっていますね.この公式にあてはめて考えれば1000番目だろうが1億番目だろうがすぐに計算できてしまうわけです.
次に『等差数列の和』の公式を見てみましょう.公式は次の通りです.
・『等差数列の和』=(初項+末項)×項数÷2
初項は最初の数,末項は最後の数のことです.項数は並んでいる数の個数のことです.
上の数列を例に,和を求めてみましょう.
まず,1番目の数(初項)は『2』です.
4番目の数は□番目の数を求める公式を使って,2+3×(4-1)=11 です.
1番目から4番目までの項数は4個です.
よって和の公式にあてはめると,
『1番目から4番目までの和』=(2+11)×4÷2=26
と求まります.たしかに,2+5+8+11=26になっています.
これは少しまちがいやすい問題です.注意して見てみましょう.
まず,3番目の数は,2+3×(3-1)=8 です.
6番目の数は2+3×(6-1)=17 です.
項数は6-2=4個 です. ←この求め方は「約数と倍数 その1」の問題2で紹介しています.確認してみてください.
では和の公式にあてはめてみましょう.この問題では,“3番目から”となっているので,初項には2ではなく,8を入れます(まちがいやすいので注意!).そして和の公式にあてはめると,
『3番目から6番目までの和』=(8+17)×4÷2=50
と求まるわけです.
この例のように,和の計算は必ずしも1番目から始まるわけではないことに注意しましょう.
等差数列以外の数列
中学入試には当然のことながら等差数列以外の数列も多数出題されます.具体的には次のような数列があります.
(それぞれの数列の問題例はまたページを改めて紹介したいと思います)
階差数列
各項の「差の差」が一定な数列です.やや応用問題です.差を二重に求める分,計算量が少し多くなります.
※階差数列の具体的な解法は→こちら(階差数列の解法)
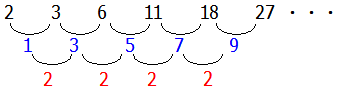
※正確には各項の差をとることによってできる数列のことを階差数列と言います(上の図だと青字の数字の並びが階差数列).
フィボナッチ数列
1番目と2番目の数を足したら3番目になり,2番目と3番目を足したら4番目になる・・・という数列です.フィボナッチ数列の一般項を求めるのは算数の領域をはるかに超えているので,答えを出すには自力で順に書き出して求めるしかありません.しかしそのせいもあって,せいぜい3~4番目の数を求めさせる問題しか出題されません.
数列としては難解ですが規則は単純なので,意外と子ども達はフィボナッチ数列を見抜くのが得意であることが多いです.
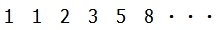
グループで区切るタイプの数列
これは出題率の高い数列です.基本的な問題から非常に難しい問題まで幅広く出題されます.区切り毎にグループで考える力と等差数列の理解力との両方が求められます.
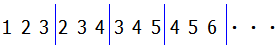
ここで注意したいのはこれらの数列については等差数列の公式が使えないということです.(等差数列ではないのですから当然ですね)
数列分野は規則性の把握が重要です.しかし,闇雲に公式の暗記に頼ってしまうと,どのようなときに公式を使い,どのようなときにどのようにグループで区切るか,などの規則性の整理が不十分となり結果的に数列がさっぱり理解できない,という事態に陥りかねません.そのようなことを避けるためにも最初のうちは多少時間をかけても規則性の正しい理解に努めるようにしましょう.
おまけ:等差数列の和の公式の説明
等差数列の公式は数少ない算数の暗記項目の中でも非常に重要な公式です.ところで等差数列の公式はなぜあのような形をしているのでしょうか?『□番目』の数を求める公式なら比較的簡単に説明できるでしょうが,複雑なのは和の公式です.ここでは等差数列の和の公式の成り立ちを見てみましょう.
等差数列の和の公式に関しては数学者ガウスの少年時代の逸話が有名です.
ガウスがまだ10才の時のお話です。
小学校の先生が次のような問題を出しました。
「1から100まで全部の数を足し算しなさい。」
生徒たちはがんばって1+2+3+・・・と順番に足し算を始めました。しかしなかなか答えは出ません。実は先生は一休みしようと思ってこんな問題を出したのでした。ところが1分もしないうちに手を挙げた生徒がいました。ガウス少年です。
「先生、できました!答えは5050です!」
おどろいたのは先生です。確かに答えは合っています。
「いったいどうやってこんなに短い時間で解いたのだい?」
先生はガウス少年に聞いてみました。
「はい先生、ぼくはこうやって・・・」
さて,ガウス少年はどのようにして答えを出したのでしょうか?
そこでまず1から100までの数を1から順に順に並べてみることから始めましょう.
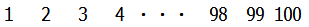
次に1から100までの数を上とは逆に100から順に並べてみましょう.
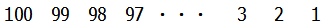
そしてこの二つを並べて,上下の数を足してみると,
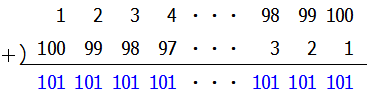
このようにすべて101になります.1から100までは数は100個あるので,101が100個並んでいることになります.
なのでこれらの和は101×100=10100 となります.
これは1から100までを2回足し合わせているので,
10100÷2=5050 となるわけです.
この例から(初項+末項)×項数÷2で等差数列の和が求まることがわかります.
ガウス少年の逸話の真偽は別として,数列の問題は「いかに効率的に解くか」が重要となります.様々な形の数列の問題に取り組み,規則性の把握とその運用の手法を学びましょう.
