階差数列の利用

数列と言えばすぐに思いつくのが各項の差が等しい「等差数列」ですが，ここでは数列の「各項の差」からできる『階差数列』が等差数列になる数列に注目してみましょう．単純な等差数列よりも計算量が多くなりますが，基本的には等差数列と同じ考え方で解くことができます．

ではさっそく具体的な問題を見てみましょう．

まず，この数列がどのような規則でできているかを確認しましょう．まずは各項の差をとってみると次のようになります．

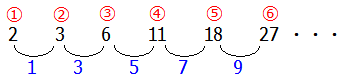
この数列の2番目の数は，

[2番目の数]＝[1番目の数]＋1＝3

と求まります．

この数列の3番目の数は，

[3番目の数]＝[2番目の数]＋3＝6

と求まりますが，[1番目の数]から考えると，

[3番目の数]＝[1番目の数]＋1＋3＝6

と書くことができます．同様に4番目の数は，

[4番目の数]＝[1番目の数]＋1＋3＋5＝11

となるこがわかります．

ここまで書くと規則が見えてきましたのではないでしょうか？例えば4番目の数を求めたかったら1番目の数に4番目の数の直前までの差をすべて足せばよいのです．

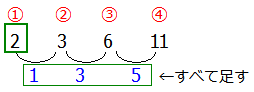
問題は『50番目の数』となっているので，この場合1番目の数に50番目の直前までの差をすべて足せば求まることがわかります．

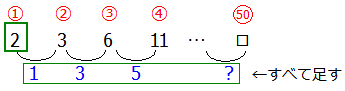
さて，求め方はわかりましたが50番目の直前の差の数がわかりません（上の図の「?」の数字）．

そこでもう一度よく上の図を見てみましょう．各項の差である青い数字は等差数列になっていることがわかります．等差数列であれば，「数列の基本」でも説明しているように，公式で求めることができます．では「?」は等差数列の何番目の数なのでしょうか？考えやすいように番号をつけてみましょう．

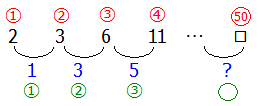
赤い数字と緑の数字を比べてみればすぐにわかります．「?」は49番目の数です．（これは50個の数の間（あいだ）の数は49個になる，という植木算の考え方に通じます）

では49番目の差の数を求めてみましょう．

初項は1，公差は2ですから，

[49番目の差の数]＝1＋2×(49-1)＝97

と求まります．

ここまで来たら答えまであと少しです．

問題の『50番目の数』は1番目の数に50番目の直前までの差をすべて足せば求まるはずです．

図の緑の枠の部分の和も公式で求めることができます．

初項は1，末項は97，項数は49ですから，

[49番目までの和]＝(1＋97)×49÷2＝2401

と計算できます．

そして最後に1番目の数に2401を足せば答えが求まります．

[求める答え]＝2＋2401＝2403　　答：2403

いかがでしょうか？等差数列に比べると階差数列を利用する数列の解法はやや複雑になりますが考え方は同じでした．ただしこの場合は，「問題で与えられている数列」と，「その差の数列（階差数列）」という二つの数列を処理しないといけないので混同しないように注意しましょう．