約数と倍数 その1
今回は「約数・倍数」に注目して,典型的な問題の考え方を見てゆきたいと思います.公約数・公倍数の基本的な意味や求め方に不安があれば,こちら(すだれ算の基本)を参考にしてください.
ではさっそく問題です.
この手の問題は約数倍数分野としては中学入試の基本的な問題です.確実に得点したいところです.
考え方ですが,まず3で割り切れない数というのは『3の倍数ではない数』のことです.7で割り切れない数というのは『7の倍数ではない数』のことです.なので3でも7でも割り切れない数というのは『3の倍数でも7の倍数でもない数』ということになります.
しかし,3の倍数でも7の倍数でもない数をいきなり求めるのは難しいです.なので,ここは逆に考えて,『3または7の倍数の数を求めて全体から引く』という方向で考えます.文章ばっかりだとよく分からなくなりそうなのでベン図で確認しておきましょう.
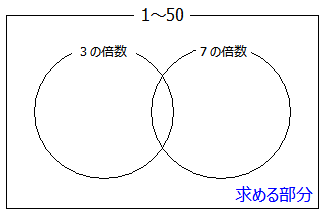
(豆知識)ベン図というのはイギリスの数学者ジョン・ベン(John Venn) が考案したものです.
さて,ベン図の中の青字で示した部分が今回求めたい部分です.1~50までは数は50個ありますので,50から3または7の倍数を引き算すればこの部分が求まるはずです.しかし,3の倍数と7の倍数には重なっている部分があります.
3の倍数でもあり7の倍数でもある数.これはまさに『3と7の公倍数』です.公倍数は最小公倍数の倍数ですので,この重なりは『21の倍数』であることが分かります.
では具体的な計算を進めてみましょう.
まず.1~50に含まれる3の倍数の個数を求めます.
50÷3=16…2
この計算の意味は,『1~50までの数を3ずつ区切っていったら16個区切りができて2個数が余った』ということです.
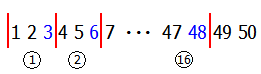
各区切りにはひとつずつ3の倍数が含まれていますので1~50までの整数の中には3の倍数は『16個』あることが分かります.(要するに余りは無視すればよいということです)
同様に7の倍数は,
50÷7=7…1
なので,『7個』ということが分かります.
次に,21の倍数は,
50÷21=2…8
なので『2個』ということが分かります.
では3または7の倍数は何個になるでしょうか?もう一度ベン図をよく見てみましょう.
3の倍数は16個.7の倍数は7個,21の倍数は2個でした.ここで『16+7=23個』と計算すると,重なりの部分を二重に足し算していることになります.そこで『23-2=21個』と計算するとダブリが消え,3または7の倍数の個数が正しく求められました.
よって答えは21個!・・・としてしまいそうですが,実はこの手の問題で一番多い誤答がこのパターンです.
問題は『3でも7でも割り切れない数』を問うているのでこれはまちがいです.
正しくは最後に,1~50の整数50個から求めた21個を引き算する必要があります.
50-21=29 答:29個
以上で解答終了です.
※ちなみに先ほどの『21個』という誤答は,問題が『1から50までの整数で,3または7で割り切れる数は何個ありますか.』であれば,正しい答となります.(これもよく中学入試で出題される)
ところでこの問題は次のような形で出題されることもしばしばです.
一見するとさっきの問題とどこが違うのか分からないかもしれません.それほど問題文としては酷似しているのですが,この問題の方が先ほどの問題より確実に難易度は上です.
この問題の場合も3,7,21の倍数の数をそれぞれ求めるのですが,例えば3の倍数を求める場合,
「50÷3=16…2」の計算では『1~50』までの数に含まれる3の倍数の個数しか求まりません.じゃあ『10~50には数が41個あるので『41÷3=13…2 ⇒ 13 個』とすればいいじゃないか!と言えそうですが,必ずしもそれが正しくない場合もあります.例えば同じ3つの数でも,7~9に含まれる2の倍数は1個ですが,8~10に含まれる2の倍数は2個です.
ですので,この場合は『1~9』と『1~50』に分けて計算することで正しい個数が求められます.
流れとしては,『1~9に含まれる個数を計算する』→『1~50に含まれる個数を計算する』→『引き算することで10~50に含まれる個数が分かる』という風になります.
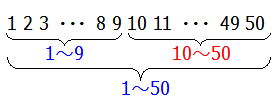
具体的な計算をしてみましょう.
まず,3の倍数は,
1~9について
9÷3=3 →3個
1~50について
50÷3=16…2 →16個
10~50について
16-3=13個
7の倍数は,
1~9について
9÷7=1…2 →1個
1~50について
50÷7=7…1 →7個
10~50について
7-1=6個
21の倍数は,
1~9について
0個
1~50について
50÷21=2…8 →2個
10~50について
2-0=2個
よって3または7の倍数は,
13+6-2=17個
10~50には数が41個(50-9=41)あるので
41-17=24 答:24個
いかがでしょう?ベン図の使い方などと共によく整理して,数えまちがいがないよう注意してください.
