約数と倍数　その２

「約数と倍数　その1」ではベン図を使って倍数が何個あるかを求める，という問題を考えました．ひとくくりに『約数・倍数』と言っても問題の形は様々あります．今回はまた別な形の約数・倍数の問題に取り組んでみたいと思います．

では問題を見てみましょう．

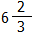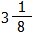問題： ，のどちらにかけても整数となる分数のうち最も小さい分数を求めなさい．

Web上で分数を表示するのって難しいですね・・・　というひとりごとはさておき，この問題も中学入試では頻出問題です．またこの問題は，分数の意味や公約数・公倍数の理解を深めることができるので個人的に良問だと思っています．

さて解き方ですが，「どちらにかけても」と言っているので帯分数を見ていても仕方ありません．とりあえず仮分数に直しましょう．

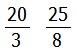
求める分数を△/□とおいてみるとこのように書けます．

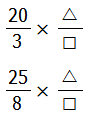
この二つの計算結果は整数にならなくてはいけません．つまり分母は約分によりすべて『1』にならないといけないのです．

左側の分数の分母3と8が約分により1になるためには△は3の倍数または8の倍数でなければいけません．また，右側の分数の分母□が1になるためには20または25で□が割り切れなくてはいけません．つまり20または25の約数でなければいけません．以上のことをまとめると次のようになります．

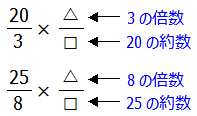
△は3の倍数でもあり8の倍数でもあります．つまり，分子は3と8の公倍数です．

□は20の約数でもあり25の約数でもあります．つまり，分母は20と25の公約数です．

さて，求める分数の分母は20と25の公約数，分子は3と8の公倍数であることまでは分かりました．しかしそれだけでは数が確定しません・・・どうしましょうか？

そこで問題をもう一度よく読んでみます．求めるのは『最も小さい分数』です．小さい分数とはどんな分数でしょう？

分数の分子は小さくなればなるほど全体としての数は小さくなります．

例：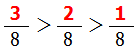

逆に分母は大きくなればなるほど全体としての数は小さくなります．

例：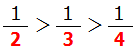

ですので△はできるだけ小さい数がよく，□はできるだけ大きい数がよいということになります．つまり，

△は3と8の公倍数なので，求める値は3と8の最小公倍数

□は20と25の公約数なので，求める値は20と25の最大公約数

となるのです．3と8の最小公倍数は24，20と25の最大公約数は5です．つまり求める答えは，

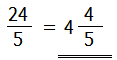
となるのです．

いかがでしたか．冒頭で「分数の意味や公約数・公倍数の理解を深めることができる問題」と述べましたが，その意味が分かっていただけたでしょうか？