すだれ算の基本
約数・倍数の概念は様々な文章題に登場するのはもちろんのこと,分数の計算をする上でも非常に重要な考え方です.「最大公約数」と「最小公倍数」をごっちゃにしないのはもちろんのこと,両者の正しい求め方を身につけるようにしましょう.
まずは簡単に「公約数と公倍数とは何か?」をおさらいしておきましょう.
公約数と公倍数
公約数と公倍数を説明する前に約数と倍数を簡単に説明しておきます.
まず,約数とは「割り切ることができる数」のことです.例えば『6』という数は1と2と3と6では割り切れますが4と5では割り切れません.なので6の約数は1と2と3と6になります.
倍数とはその数を自然数倍した数(注1)のことです.例えば『3』を2倍,3倍,4倍・・・した数,すなわち「6,9,12」などは3の倍数です.約数と違って倍数は無限に存在します.
さて,公約数と公倍数に戻りましょう.公約数とは2つ以上の自然数に共通な約数のことです.もっとわかりやすく言うと,「両方とも割り切れる数」のことです.例えば『12と6』は両方とも1,2,3,6で割り切れます.なので1,2,3,6は12と6の公約数であると言えます.また,最も大きい公約数のことを『最大公約数』と言います(12と6の場合は『6』です).最大公約数には覚えておきたいひとつの特徴がひとつあります.それは,『公約数は最大公約数の約数となる』ということです.12と6の最大公約数は6でした.6の約数は「1,2,3,6」です.たしかに12と6の公約数と一致しています.
次に公倍数です.公倍数は2つ以上の自然数に共通な倍数のことです.もっとわかりやすく言うと,「両方の数を何倍かした数」です.例えば『4と6』の公倍数を考えてみましょう.4の倍数は 4,8,12,16,20,24…と続きます.6の倍数は6,12,18,24…と続きます.ここで『12』や『24』は両方の倍数に表れていることが分かります.この12や24が4と6の公倍数です.また,最も小さい公倍数のことを『最小公倍数』と言います(4と6の場合は『12』です).最小公倍数にも覚えておきたいひとつの特徴があります.それは,『公倍数は最小公倍数の倍数である』ということです.4と6の最小公倍数は12でした.12の倍数は12,24,…ですからたしかに4と6の公倍数に一致しています.
(注1) 自然数:「1,2,3…」と続く整数.受験算数では通常0は含まない.
すだれ算で最大公約数と最小公倍数を求める
最大公約数や最小公倍数がどんなものかをおさらいしたところで,次に,じゃあどうやって最大公約数・最小公倍数を求めるの?というところに移りましょう.最大公約数や最小公倍数には,『すだれ算』という便利な求め方があります.ここではすだれ算のやりかたを解説します.
すだれ算とは割り算を繰り返し実行する計算のことです.通常の割り算の筆算と違って逆方向に進むので子ども達からは『逆割り算』と呼ばれることもあります.
では具体的に『6と12』の最大公約数をすだれ算で求めてみましょう.
まず6と12を並べて書いて割り算の筆算と逆の線を引きます.6と12はどちらも2で割り切れるので左側に『2』と記入して,6と12の下には2で割り算した結果(3と6)を書きます.
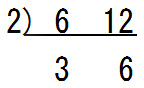
3と6はどちらも3で割り切れるのでさらに計算を続けます.
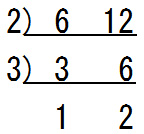
1と2はもうこれ以上は割り切れないので,すだれ算はここで終了です.
次に6と12の最大公約数ですが,これは左側の数を掛け算した数になります.
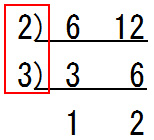
赤枠で囲った部分を掛け算して『2×3=6』が6と12の最大公約数なのです.
最小公倍数を求めるときには
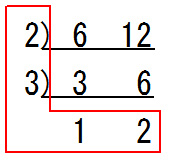
このようにL字型になるように数を掛け算します.
赤枠で囲った部分を掛け算して『2×3×1×2=12』が6と12の最小公倍数です.
いかがですか?案外単純作業で求められるでしょ?
ちなみにすだれ算の計算は一通りではありません.6と12は両方6で割り切ることができる,ということに気付けば,いきなり6から計算を始めてもかまいません.
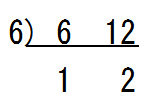
これだと1回ですだれ算終了になりますが,最大公約数・最小公倍数は同様にそれぞれ6と12であることが確認できます.
すだれ算は割り切ることのできる数ならどれからでも始めてかまいません.ただし,そこで注意したいのは『まだ計算できないか十分にチェックする』ということです.例えばすだれ算で繰り返し計算した結果『26と39』という数になったとしましょう.この2つの数はいかにもこれ以上割り切れなさそうですが,実は両方とも13で割り切ることができます.
以上が基本的なすだれ算の考え方です.「まだ計算できないかよく確かめる」「最大公約数と最小公倍数の計算は,すだれ算終了後の最後の掛け算だけが異なる」の2点に注意してよく練習しておきましょう.
2つの数のすだれ算に慣れてきたら,次は3つの数のすだれ算にチャレンジです!
※なお,『確実に』最大公約数を求める方法として,「ユークリッド互除法」という計算方法もあります.中学受験算数では用いない考え方ですが,計算自体は単なる割り算なので興味のある方はご覧ください.
