３つの数のすだれ算

２つの数の最大公約数と最小公倍数をすだれ算で求める方法は「すだれ算の基本」で紹介していますが，今回は３つ（または３つ以上）の数のすだれ算の解説です．

２つの数の場合と異なり，３つ以上の数の場合は最大公約数と最小公倍数で求め方が異なるので，間違えないよう十分注意しなくてはいけません．

中学受験算数の問題で４つ以上の数の最大公約数・最小公倍数をすだれ算で求めることが必要とされる場面はほとんどありません．なのでここでは３つの数の場合で解説することにします．

３つの数のすだれ算（最大公約数）

まずは最大公約数の求め方から見てみましょう．ここでは具体的に『9，12，18』の場合を考えてみましょう．

３つの数の最大公約数を求める際はやはり，『３つの数が共通して割り切れる数』を探します．「9，12，18」の３つの数をじっと見つめるとその数は『3』であることに気付きます．なのですだれ算は次のようになります．

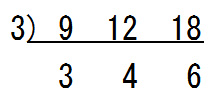
『3，4，6』にはこれ以上共通して割り切ることのできる数はありません．ですので，9，12，18の最大公約数は『3』であることが分かります．

３つの数のすだれ算（最小公倍数）

３つの数の最大公約数は２つの数の場合と同じ考え方でしたが，３つの数の最小公倍数の求め方は少し異なります．

先ほどと同様に『9，12，18』を例に考えてみましょう．9，12，18は３つとも『3』で割り切れるのでまずは3で割ります．

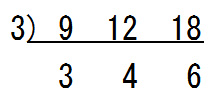
ここまでは最大公約数の求め方と同じです．最小公倍数の求め方が違うのはここからです．

上の計算では3で割った結果が『3，4，6』となっています．3，4，6を共通して割り切ることのできる数はありませんが，4と6だけ見ると2で割り切れます（3と6を見ても3で割り切れます）．３つの数の最小公倍数を求めるときは，このような『２つの数だけで割り切れる』場合も計算を進めるのです．

まずは4と6を2で割ってみましょう．

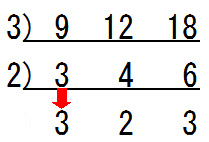
このとき『2』で割り切ることのできない『3』はそのまま下に移動させるのがポイントです．

次に，この計算により求まった『3，2，3』をさらに3で割ってみましょう．このとき『2』は3で割り切れないのでそのまま移動させます．

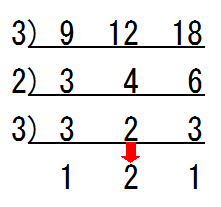
「1，2，1」はたとえ２つの数を取ってみてもさすがにこれ以上割り切ることができる数はありません．

よってすだれ算はここで終了です．

最小公倍数はＬ字型の掛け算で求めますので『3×2×3×1×2×1＝36』が最小公倍数であることが分かるのです．

ここで注意したいのは最小公倍数を求めるために行ったすだれ算を使って最大公約数を求めることはできないということです．仮に今のすだれ算で最小公倍数を求めてしまうと『3×2×3＝18』という誤った答えが出てきてしまいます．（逆もしかり；最大公約数を求めるすだれ算で最小公倍数を求めることはできません）