ユークリッド互除法を図で考える

ユークリッド互除法はこちらで解説している方法で式にあてはめてさえいけば機械的に求めることができます．しかし，計算の意味を理解せずに利用するのはあまり好ましいことではありません．

ここではユークリッド互除法の計算の意味を図を描きながら考えてみることにします．

ここでは前の例と同じ「221と323」で考えてみましょう．

これを式で求めると，

① 323 ÷ 221 ＝ 1・・・102
② 221 ÷ 102 ＝ 2・・・17
③ 102 ÷ 17 ＝ 6

答え：17

となりました．

この計算を次のような長方形を使いながら考えてみます．

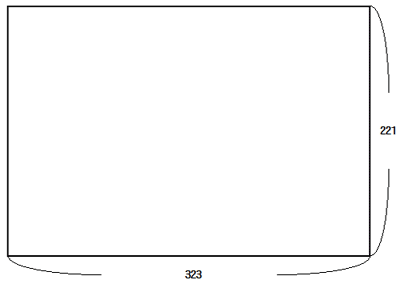
221と323の最大公約数を求めるというのは，「この長方形を最も大きな正方形でぴったり埋めようとしたとき，その正方形の一辺はいくらになるか」という問題に置き換えられます．

①の計算は，まずこの長方形の中に「最も大きな正方形をつくってみる」ことを示しています．これを図で表すと次の通りです．

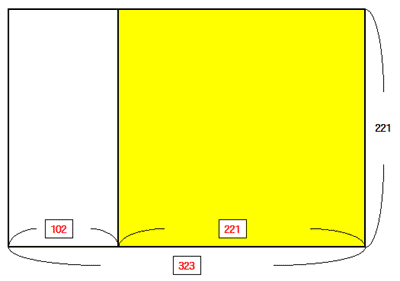
上の図で黄色で示しているように，「最も大きな」正方形の一辺はこの長方形の短辺，すなわち221になります．
ですので①の式「323 ÷ 221 ＝ 1・・・102」は，「この長方形には一辺の長さが221の正方形が１つだけ入り，横102,縦221の長方形が余る」ことを示していることになります．

同様に②の計算は，「①の計算で余った横102,縦221の長方形の中に最も大きな正方形をつくってみる」ことを示しています．これを図で表すと次の通りです．

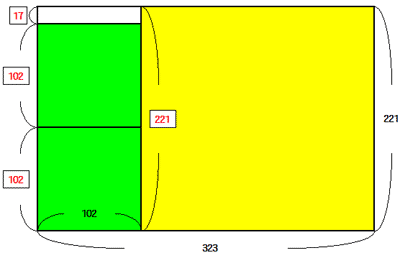
上の図で緑色で示しているように，「最も大きな」正方形の一辺は余った長方形の短辺，すなわち102になるので，②の式「221 ÷ 102 ＝ 2・・・17」は，「この長方形には一辺の長さが102の正方形が２つ入り，縦17,横102の長方形が余る」ことを示しています．

③の計算も同様に，「②の計算で余った縦17，横102の長方形の中に最も大きな正方形をつくってみる」ことを示しています．これを図で表すと次の通りです．

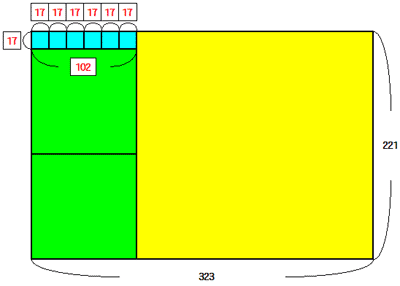
上の図で水色で示しているように，「最も大きな」正方形の一辺はこの長方形の短辺，すなわち17になるので，③の式「102 ÷ 17 ＝ 6」は，「この長方形には一辺の長さが17の正方形がちょうど６つ入る」ことを示しています．

このことから，最初の縦221，横323の長方形を最も大きな正方形でぴったり埋めるとき，そのときの正方形の一辺は17である，すなわち221と323の最大公約数は17であることが分かるのです．