速さと比の演習(平均の速さ)
平均の考え方についてはこちら(『平均』の計算に注意!)で紹介していますが,速さと比の分野にも「平均の速さ」というものが登場します.ここでは平均の速さについて考えてみます.
ではさっそく問題です.
行きは時速5km,帰りは時速3kmなので,(5+3)÷2=4 → 時速4km,とすると間違いです!
こちら(『平均』の計算に注意!)では,男女の平均点を求めるときに「足して2で割る」のがいけないのは,「男女の人数が同じではない」からでした.
ではこの問題の場合はどうでしょう?同じ道を往復しているので行きも帰りも「道のり」は同じです.なら,この場合は足して2で割ってもいいのでは??と考えてしまいそうですが,ちょっと待ってください.行きと帰りではかかった「時間」が違います.
平均の速さの求め方は次の通りです.
平均の速さ=道のりの合計÷時間の合計
平均の速さだからといって特別な公式はありません.速さの求め方と基本的には同じです.
この問題の場合,「道のりの合計」は
12×2=24kmです.
「時間の合計」は往復それぞれにかかった時間を合計します.
行き:12÷5=2.4時間
帰り:12÷3=4時間
よって時間の合計は2.4+4=6.4時間です.
以上より,平均の速さは,
24÷6.4=3.75 → 時速3.75kmとなります.
さて,『平均の速さ』が真価を発揮するのは次のような問題の場合です.
行きと帰りでは帰りの方が時間が長くなっています.ということは,ここから,「帰りの方が登り道が長かった」ということが言えます.
これはつまり,A~峠と峠~Bでは峠~Bの方が距離が長いということです.
この様子を図に表してみましょう.
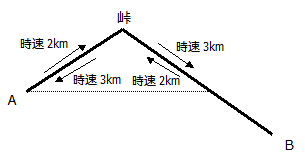
峠~Bの途中で,A~峠と距離の等しい地点をCと置いてみます.
するとA→峠→CとC→峠→Aにかかった時間は等しくなるので,往復の時間差(4-3.5=0.5時間)はC~B間の往復で生じたことになります.
C→BとB→Cの速さの比は3:2なので時間の比は2:3となります.そこで,かかった時間をそれぞれ②,③と置くと,
③-②=①が0.5時間にあたることになります.
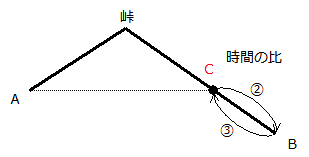
①=0.5時間なので,
C→Bに要した時間は②=0.5×2=1時間です.
C→Bは時速3kmで進んだので,C~B間の距離は
3×1=3km となります.
一方,A→峠→Cに要した時間は3.5-1=2.5時間になります.
A~峠と峠~Cは同じ距離なので,
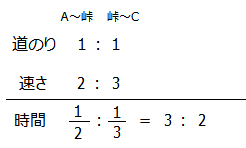
となります.
よってA→峠に要した時間は
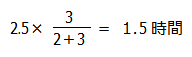
よって,
A~峠の距離は2×1.5=3km となります.
峠~Cの距離はA~峠と等しいので,3kmです.
以上をまとめると,A~B間の距離は
3+3+3=9kmとなります.
ずいぶん長くなりましたが,正攻法でいくと以上のような解答になると思います.
もちろん,問題によってはこのような考え方も大事です.(特に『A~峠より峠~Bの方が距離が長い』ことを考えるという点)
ただし,この問題の場合は『平均の速さ』を用いると,もっと簡単に解くことができます.
この問題では,登りと下りで歩く速度が異なっていますが,『登りと下りの平均の速さ』を求めてみましょう.
登りは時速2km,下りは時速3kmなので,最小公倍数の6kmの区間で計算してみます.
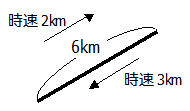
この区間の往復距離:6×2=12km
この区間の往復時間:6÷2+6÷3=5時間
よって登りと下りの平均の速さは
12÷5=2.4 →時速2.4km となります.
よって,この問題は「時速2.4kmでずーっと歩き続けると,3.5+4=7.5時間で往復できた」と言い換えることができます.
往復の距離は2.4×7.5=18kmなので,片道は18÷2=9kmと求めることができるのです.
このように,平均の速さを利用することで,ずっと素早く解答することができます.
ただし,このような解答ができるようになるには「平均の速さ」に対する深い理解が必要です.
平均の速さの意味をよく理解していないと,この問題の場合,平均の速さが時速2.4kmと求まった後に次のようなミスをしがちです.
行きは3.5時間かかったので2.4×3.5=8.4km→答:8.4km (誤)
あるいは,帰りの時間は4時間だったので,2.4×4=9.6km ・・・あれ?行きで計算した距離(8.4km)と一致しない・・・??
これらの間違いの原因に気付けないうちに,平均の速さをむやみに使うのは危険かもしれません.
ちなみにこの間違いは「登り道と下り道の長さが同じ」という誤解によって生じます.
A→峠→B→峠→Aと往復したときには全体として「登り道と下り道の長さが同じ」すなわち平均の速さが使用可能ですが,
A→峠→B,あるいはB→峠→Aの片道では「登り道と下り道の長さが同じではない」ので平均の速さは使えないのです.
