速さと比の基礎知識
速さと比の問題は中学受験算数では極めて重要な分野です.単純な計算から複雑な文章題まで応用範囲が非常に広いので,出題される問題にも様々なパターンがあります.ここではまず,速さと比に関する基本事項を確認しておきましょう.
まずは速さに関して確認しておきたい公式です.
- 「速さ」=「道のり」÷「時間」
- 「道のり」=「速さ」×「時間」
- 「時間」=「道のり」÷「速さ」
似たような公式が「食塩水と比」にも登場します.公式は3つありますが,重要なのは1番目の公式です(正確に言うと,公式ではなく「速さ」の定義そのものです).これさえ覚えておけば2番目と3番目の式は自力で導き出せます.ただし,速さの問題では計算量が多くなりがちなので,2番目と3番目の式もサッと出せるようにしておいたほうが良いでしょう.式で覚えられないなら次のような面積図で覚えましょう.
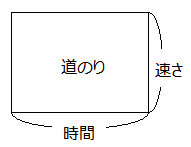
例えば3時間で60km進んだとします.これを面積図にあてはめると次のようになります.
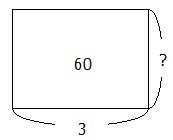
ここから速さを求めるには,面積を横の長さで割ればよいので60÷3=20→時速20kmであることがわかります.
速さの公式に関しては「食塩水と比」と同様に次のような『テントウムシ』を書くこともあります.
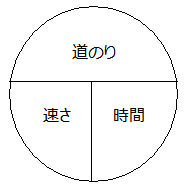
円に縦と横の線を引くことで「テントウムシ」っぽくなるわけですが,「縦線は掛け算」を,「横線は割り算」を表します.よって,わからないところ,例えば時間がわからないときは,テントウムシの「時間」の部分を隠してみると「道のり」と「速さ」が横線に挟まれます.つまり「道のり」÷「速さ」で「時間」が求まるという仕組みです.
ただし,この「テントウムシ」を使うことはあまりお勧めしません.なぜなら,テントウムシはあくまでも「公式をわかりやすく表している」だけであり,図そのものには何の意味もないからです.その点,面積図は比の概念そのものを表しており,速さと比の問題で多用するのはもちろん,全分野にも応用できる「価値ある図」だからです.特に,つるかめ算がからんでくると,面積図でなければ問題の様子を図に表すことができません.
速さと比では覚えておきたいもうひとつの重要な考え方があります.それが「単位」です.一口に「速さ」といっても,「時速」と「分速」と「秒速」の3つが存在します.「時間」にも「時間」と「分」と「秒」の3つが存在します.「道のり」にも「km」や「m」など様々あります.これらをごちゃ混ぜにして計算することはできません.
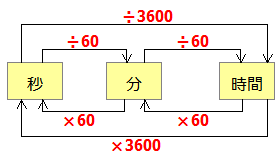
「時速」を「分速」に直すとき,「秒速」を「時速」に直すときなどには次のような計算をします.
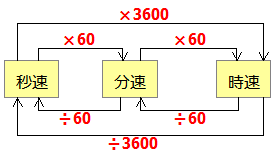
「秒速」とは正確にいうと『1秒間に進むことができる道のり』のことです.「分速」とは『1分間に進むことができる道のり』です.1分は60秒なので上の図のように,速さを変換する際には「×60」や「÷60」が登場するのです.
例えば『時速30kmで20分進みました.進んだ道のりは何kmですか』という問題があったとします.
このとき,道のりは「速さ×時間」だからといって,「30×20=600km」と計算するとまちがいです.
なぜなら速さと時間で単位が異なっているからです.
時速は「1時間に進むことができる道のり」なので時間をかけるときに「分」ではいけません.必ず「時間」でないといけないので,まずは20分を時間に変換します.
「分」を「時間」や「秒」に直すには「速さ」と同様の計算が必要です(×と÷が速さの変換とは逆になるのに注意).
20分を時間に直すと20/60=1/3時間となります.よって道のりは「30×1/3=10km」と計算できるわけです.あるいは時速を分速に直して,30÷60=0.5→分速0.5kmとし,道のりを0.5×20=10kmと求めても構いません.
上の問題では「道のりは何kmですか」と聞いていますが「何mですか」と聞かれることも多くあります.1km=1000mなので(詳しくは「覚えておきたい単位換算」を参照),この場合は最後の答えである10kmを10000mとすれば良いだけですが,次のような問題の場合は注意です.
「3500mの道のりを時速10kmで進みました.何分かかりましたか」
時間を聞いているからといって,「3500÷10=350分」と計算してはいけません.いま時速は「km」で表わされているので3500mを3.5kmに直しておく必要があります(あるいは時速10kmを時速10000mにする).よって3.5÷10=0.35時間(または3500÷10000=0.35時間)となり,さらに「時間→分」の変換をしなくてはいけないので,0.35×60=21分が答えとなります.
