当サイトは受験生のお子様を持つ方々,中学受験算数を教えている・教えたい方々,算数・数学が好きな方々,など幅広い『大人のための』中学受験算数解説サイトです.
食塩水と面積図2
食塩水における面積図の使い方の基本は食塩水と面積図1で確認しました.ここでは面積図を使うやや応用問題に取り組んでみることにします.
ここでは「食塩水の移し替え2」で解説した問題の変形バージョンを見てみましょう.
問題:容器Aには4%の食塩水480g,容器Bには2%の食塩水800gが入っています.2つの容器から同じ量をくみ出しAの分をBに,Bの分をAに同時に入れ替えるとAの食塩水の濃度は3.5%になりました.くみ出した食塩水は何gですか.
食塩水の移し替え2ではBの濃度は何%?という問題でしたが,今回は「くみ出した食塩水の量」が問題です.これは下のようなビーカー図を見ていても解答の糸口がつかめなさそうです・・・
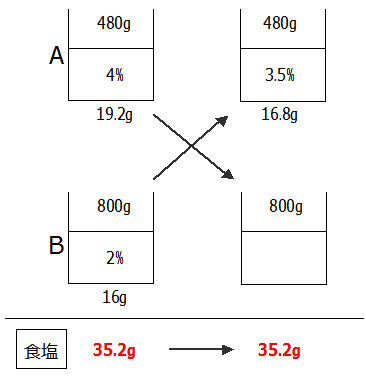
というわけで,この問題は面積図を使って考えてみましょう.
とりあえず食塩水Aに注目してみましょう.
Aから何gか抜き取られた後,同じ量のBが入ってくるのでAの食塩水の重さは480gのまま変わりません.
Aの濃度は4%,Bの濃度は2%と分かっているので面積図は次の通りです.
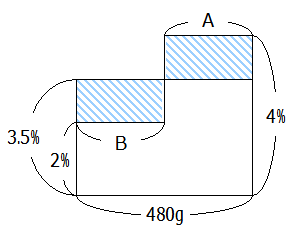
この面積図における「B」の食塩水の量が求める答えになります.
斜線部の縦の長さの比は計算することができます.
(4-3.5):(3.5-2)= 0.5:1.5 = 1:3
よってA:Bはその逆比で3:1となります.

AとBの合計は480gと分かっているのでこれを比例配分してBの量を求めます.
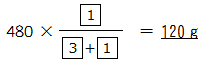
よってA,Bそれぞれ120gずつ入れ替えたということになるのです.
食塩水と面積図1の例題は計算でも解くことができましたが,今回の問題は面積図を描き,比を用いた計算をしなければ答えにたどり着けません.逆に面積図を描くことで求める部分が視覚的にも分かりやすくなり,そこにたどり着くための道筋も見えてくるというわけです.
関連情報
