食塩水と面積図1
「食塩水を混ぜる」問題では面積図を活用できます.濃度の違う食塩水を混ぜ合わせるということは要するに濃度が平均化されるということです.つまり,『平均』の計算に注意!でも確認したのと同じ方法で食塩水の問題も考えることができるのです.
具体的な問題を見てみましょう.
この問題そのものは面積図を描かず,計算で求めることもできます.
200×0.05=10g
300×0.1=30g
10+30=40g
40÷(200+300)×100=8% という具合です.
これを面積図で表してみます.
食塩水と比の基礎知識で確認したとおり,面積図は縦に濃度,横に食塩水の量を書きます.
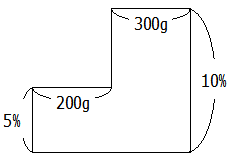
これを混ぜ合わせる(平均する)と次のようになります.
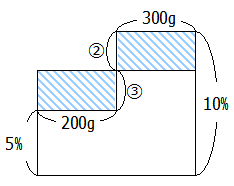
斜線部は面積が同じなので,横の長さの比の逆比が縦の長さの比になります.
横は200:300=2:3なので縦の比は3:2となります.
②+③=⑤が10-5=5%にあたるのでこれを比例配分します.
③にあたる量を求めると,
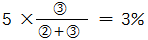
よって求める濃度は5+3=8%となります.
今回は面積図の基本を確認するため,計算でも求められる問題を例題にしましたが,面積図を使う(比を使う)ことで計算が簡略化できますし,問題によっては計算では求められない(比でしか解けない)ときもあります.
食塩水の問題ではほとんどの場合,ビーカーの図か面積図を描くことで解くことができるので合わせてよく確認しておきたいところです.
食塩水を混ぜ合わせる問題では面積図ではなく,天びんを使って教える場合があります.
上の問題を天びんで考えると次のようになります.
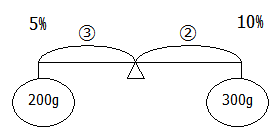
天びんの釣り合いは理科でも習いますが,食塩水の問題では「おもり」を「食塩水の重さ」,うでの長さを「濃度」として考えます.そして,混ぜ合わせたときの濃度が支点での濃度になります.
天びんのうでの長さは重りの比の逆比になります.うでの長さは10%-5%=5%なのでこれを比例配分します.すると支点の濃度は先ほどの計算と同様に考えて,
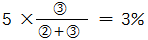
よって支点の濃度は5+3=8%となります.
・・・以上が天びんの考え方です.お気づきかもしれませんが,この天びん図は面積図の縦の長さを横向きに描いたものです.
面積図よりも図が簡単なので,この方法で教わる生徒も比較的多いのですが,当サイトでは天びんを使うことはお勧めしません.
なぜならば,天びんの図は他に応用できない特殊な考え方だからです.一方面積図は他にも応用できる汎用的な図であり,視覚的にも分かりやすいので,当サイトとしては面積図で統一して考えることを勧めます(どっちつかずに両方使おうとすると余計に混乱してしまいます).
