食塩水の移し替え２

「食塩水を移し替える」問題の解基本的な考え方は『食塩水の移し替え１』で確認しましたが，ここでは同じような問題の少し応用編を考えてみましょう．

さっそく問題です．

問題そのものは食塩水の移し替え１と似ていますが，何g移したのかが分からないところが少し応用問題になっています．

この問題では「変わらない量」に注目することが大切です．「変わらない量」に注目することは和差算の演習でも紹介しているように，色々な場面で登場します．

ではさっそく図に表してみることにします．

Aの食塩の量は，480×0.04＝19.2g

Bの食塩の量は，800×0.02＝16g　です．

また，A，Bの食塩水の入れ替えは同じ量ずつ行っているので，入れ替え後A，Bとも食塩水の量は変わりません．

入れ替え後，Aの濃度は3.5％になったので，食塩の量は，

480×0.035＝16.8g

となります．

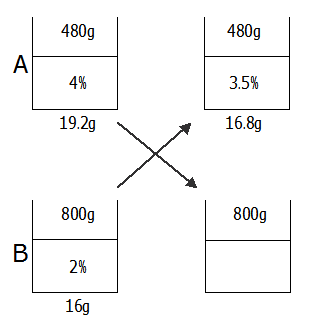
図には描けましたがBの食塩の量が分からないので濃度が計算できません・・・．

そこで，『変わらない量』に注目です．この入れ替えの操作ではA,Bの全体の『食塩の量』は変わりません．

最初の食塩の量の合計は19.2＋16＝35.2gであり，この量は入れ替え後も変わりません．

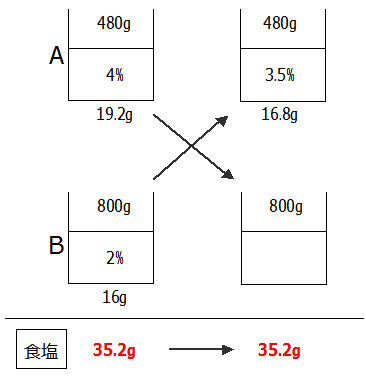
入れ替え後，Aの食塩の量は16.8gなので，Bの食塩の量は35.2－16.8＝18.4gです．

よって，Bの濃度は18.4÷800×100＝2.3％となります．

「変わらない量に注目する」ことは食塩水の問題に限らずあらゆる場面で登場する大事な考え方ですので，よく確認しておきましょう．逆に「変わらない量」にすぐ着目できるようなれば「算数マスター」に一歩近づけたとも言えるのです．