速さと比(時計算その１)

中学受験算数では，時計に関する問題もよく出題されます．●時●分のときの長針と短針の角度を求めよ，とか，長針と短針が重なる時刻を求めよ，などなど．

一般的にはこういった問題を「時計算」と呼びますが，時計算は旅人算の一種です．そもそも時計というのは，動きの早い長針と，動きの遅い長針が同じ方向にグルグル回っている機械です．ということは，これは池の周りをグルグルまわる問題と基本的には同じということになります．ただし，池の周りを回る問題では「長さ」を問題にしていましたが，時計算では「角度」を問題にしているという点が少し異なります．

時計算では覚えておきたいことが3つあります．

（正確には，覚えなくても自力で導き出せますが，覚えておいた方が時間の節約になります）

まず1点目は時計の目盛についてです．

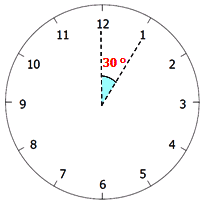
時計には1から12までの数字が書かれていますが，この1目盛分(1時間)の角度は，

360÷12＝30°　となります．

次に覚えておきたいのが（こちらの方が重要です）『長針，短針がそれぞれ１分間に動く角度』です．

長針は60分で360°動きますから，1分につき，360÷60＝6°動きます．

長針は60分で30°動きますから，1分につき，30÷60＝0.5°動きます．

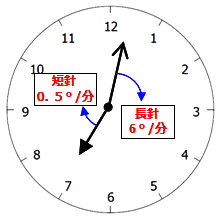
以上3つの数値は覚えておくようにしましょう．

なお，余裕があれば次の小数→分数の変換も覚えておきたいところです．

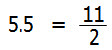
なぜ，この変換を覚えておいたほうがよいかというと，長針と短針は同じ方向に動くので「6－0.5」の計算をすることが非常に多く，さらに，時計算では答えが分数になることが多いので，5.5を分数に直して計算することが多いからです．

時計算以外では答えが中途半端な分数になったときは計算ミスを疑いたくなりますが，時計算の場合はむしろ中途半端な分数ばっかりです．

時計算でよくある『長針と短針がちょうど●°になるときの時刻』というのは，ほぼ確実に中途半端な分数になります．

以上をふまえて，まずは基本問題です．

時計算は基本的に図を描きながら解いていきます．その際，時計を正確に描く必要はまったくありません．必要な部分さえしっかりわかる図であればそれでよいのです．

※以降は，長針と短針の区別がつくように，長針は，短針は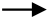で表わすことにします．

まず，6時ちょうどだと，長針と短針の角度は180°です．

30×6＝180°

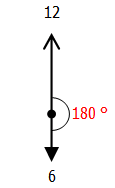
これが，6時50分になると，長針と短針はそれぞれ次の角度だけ動きます．

長針：6×50＝300°

長針：0.5×50＝25°

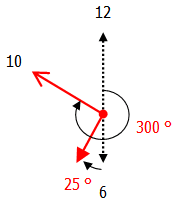
よって，6時50分での長針と短針の作る角度は，

300－(180＋25)＝95°　となります．

このとき，図を見ながら，あるいは腕時計を見ながら，6時50分を思い浮かべてみてください．イメージ的にも長針と短針は95°くらいなので，答えはこれで正しそうですね．

5時ちょうどのときは，長針と短針の作る角度は，

30×5＝150°　です．

この150°開いた状態から，長針が短針を追いかけます．そして，長針が短針に追いついたとき（角度が0°になるとき）の時刻が求める答えとなります．

長針は毎分6°，短針は毎分0.5°で動くので，

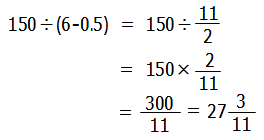
よって求める答えは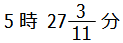，　となります．

このとき，問題１のときと同じように，5時と6時の間で針が重なるときを思い浮かべてみてください．イメージ的にもだいたい5時25分過ぎくらいだと思いませんか．ということは，これで答えは正しそうです．

よく，「受験会場にはアナログの腕時計をしていったほうが良い」と言います．

これには理由がいくつかあります．ひとつは，アナログの方が「残り時間がわかりやすい」からです．デジタルだと残り時間は計算しなければなりませんが，アナログだと，視覚的にあとどれくらい時間が残っているかがつかみやすいのです．また，変に多くの機能を有するデジタル時計は計算機と同じと見なされて外すよう指示されるかもしれません．そして何より，アナログ時計は時計算に有利です．時計算では今回紹介した問題１，２のように，求める答えのおおよその数値を想像できることが多いです．計算した結果と想像とが大きく異なれば，この計算は間違っているという，簡単なチェックができるわけです．このとき，時計を見ながら想像することができればさらに有利です．受験会場にも時計は備えられているでしょうが，使い慣れた時計を手元でチェックするほうが良いので，受験会場にはアナログ時計を持って行けというわけです．