速さと比の演習(平均とつるかめ算の応用)

『平均の速さ』考える問題や『つるかめ算』になるタイプの問題に続いて，ここではその両方を利用する応用問題に取り組んでみたいと思います．

さっそく問題です．

この問題の基本的な考え方は「速さと比の演習(平均の速さ)」の問題2と同様です．

解法には2通りありますが，ここではよりシンプルに「上りと下りの平均の速さ」を使う方法で考えてみましょう．

今，上りは時速3km，下りは時速5kmなので，最小公倍数の15kmで計算してみます．

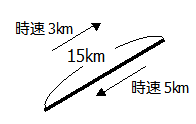
この区間の往復距離：15×2＝30km

この区間の往復時間：15÷3＋15÷5＝8時間

よって上りと下りの平均の速さは

30÷8＝3.75 →時速3.75km　となります．

よって，この問題は「往復で25km×2＝50kmの道のりについて，坂道は時速3.75km，平らな道は時速4kmで進むと，6時間20分＋6時間40分＝13時間で往復できた」と言い換えることができます．

もうお気づきかと思いますが，これはもう典型的なつるかめ算ですよね．

求めたいのは平らな道の道のりですので，平らな道を進んだ時間を□とすれば答えが求められそうです．

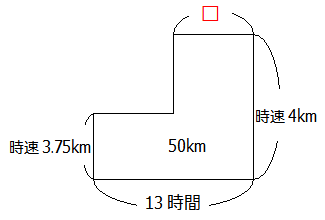
□を求める式をひと続きで書くと，

(50－3.75×13)÷(4-3.75)＝5時間

となります．

平たんな道は時速4kmで進んだので4×5＝20kmが答え！・・・としてしまうのは尚早です．

なぜなら，今は『往復』で考えているので，この20kmというのは平たんな道を往復したときの道のりです．

よって，正しい答えは20÷2＝10kmとなります．

平均の速さとつるかめ算をよく理解していればそれほど難しい問題ではないのですが，最後の答えで2で割ることを忘れないよう注意したいところです．

この問題には解法が2通りあり，ここでは簡単な方で説明しました．もうひとつは，具体的にA-B間の図を描いてみて，2つの坂はどちらが長いか，また，往復の時間差はどこで生じているか，を考えていく方法です．余裕があればこの考え方で解いてみるのもよいと思います．計算量は多くなりますが，この考え方も非常に重要です（ただし，この考え方で解いていっても最終的には平均の速さとつるかめ算は使わないといけません）．