速さと比(旅人算の基本)

速さと比の問題には色々な種類がありますが，よく出題されるものに「2人が追いついたり追い越されたりする問題」いわゆる『旅人算』があります．

ただし，一言に旅人算と言ってもその問題パターンは無限にあり，解答方法も問題ひとつひとつに合わせていく必要があります．つまり旅人算では問題をよく読み「注意深く動きを見守ること」が大切になってきます．

旅人算の最も基本的な形は次のような問題です．

このように，２人が「出会う」地点を求める問題のことを，旅人算の中でも特に「出会い算」と呼びます．

解答はいたってシンプルです．

太郎と次郎は向かい合って進んでいるので，２人の距離は1時間に，3＋2＝5kmずつ縮まります．

A―B間は10km離れているので，２人が出会うまでにかかった時間は，

10÷5＝2時間　となります．

問題はA地からの「距離」を聞いているので，これはA地から出発した太郎に注目すれば求まります．

時速3kmで進む太郎は，A地を出発して2時間後に次郎と出会ったので，求める距離は，

3×2＝6km

となります．

このように，ある者がある者に「追いつく」地点を求める問題のことを，旅人算の中でも特に「追いつき算」と呼びます．

こちらの解答も出会い算と同様いたってシンプルです．

次郎が出発した時点で，太郎はすでに時速3kmで2時間進んでいるので，２人の距離は，

3×2＝6km　になっています．

太郎と次郎は同じ向きに進んでいるので，２人の距離は1時間に，6－3＝3kmずつ縮まります．

よって次郎が出発してから太郎に追いつくまでの時間は

6÷3＝2時間　となります．

この2時間で次郎が進んだ距離が求める距離となるので，答えは

6×2＝12km

と求まります．

さて，旅人算は上記2問のような単純な動きの問題ばかりではありません．時に非常に複雑な動きを扱うこともあります．

そんなときに便利なのが『進行グラフ』です．

進行グラフとは縦軸が距離，横軸が時間のグラフのことで，文章だけでは分かりにくい複雑な動きも進行グラフに表わすと分かりやすくなることがあります．また，進行グラフがあらかじめ描かれていて，それを見ながら解答する問題もあります．

例えば，上記の問題(1)の太郎と次郎の動きを進行グラフで表わすと次のようになります．

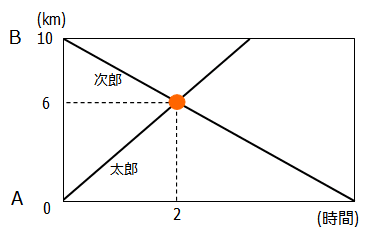
図の交点で太郎と次郎が出会っていることが分かります．

この程度の問題では進行グラフを描いても，分かりやすい！という感覚はないかもしれませんが，次のような問題だとどうでしょう．

この問題は先の問題のように動きが単純ではないので，進行グラフの描き甲斐(?)がありますね．

進行グラフを描く前に少し計算をしておきましょう．

兄は1km進んでいるので，それにかかった時間を求めておきます．

1km＝1000mなので，

1000÷50＝20分　となります．

ではこれを進行グラフに表わしてみます．

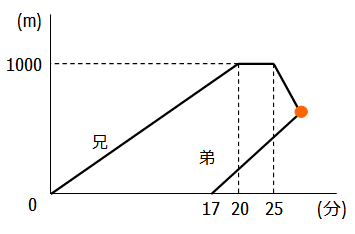
進行グラフより25分時点での２人の距離が分かれば解答にたどり着けそうです．

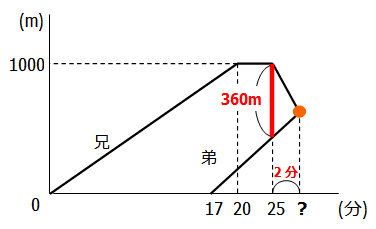
弟は25分時点ですでに25－17＝8分進んでいるので，その距離は，

80×8＝640m　です．

よって２人の隔たりは，

1000－640＝360m　であることがわかります．

兄と弟は向かい合って進む(出会い算)ので，２人が出会うまでにかかった時間は，

360÷(100＋80)＝2分

となります．

（※兄の速さは分速100mであることに注意です）

よって兄が9時に家を出発してから２人が出会うまでの時間は，

25＋2＝27分　となります．

問題は「何時何分か」を聞いているので答えは，9時27分と求まります．

進行グラフというのは旅人算のみならず，「物の動き」を表わす最も基本的なグラフです（高校の物理などにも頻繁に登場します）．進行グラフを描くことは，問題の様子を視覚化できるだけでなく，時には図形的に相似比を用いて問題を解くこともできるなど，けっこう応用範囲も広いです．

文章題では線分図，食塩水の問題では面積図を考えてみるのと同じ感覚で，物の移動に関する問題なら進行グラフを描いてみる，といったことがスムーズにできるよう，進行グラフの見方・描き方をよく確認しておきましょう．