当サイトは受験生のお子様を持つ方々,中学受験算数を教えている・教えたい方々,算数・数学が好きな方々,など幅広い『大人のための』中学受験算数解説サイトです.
速さと比の演習(歩数と歩幅)
今回は数多き速さと比の問題の中でも,比較的ややこしい「歩数と歩幅」に関する問題の解法を確認してみます.
「歩数と歩幅」とは次のような問題です.
問題:太郎くんが7歩で進む距離を次郎くんは6歩で進み,太郎くんが6歩進む間に次郎くんは7歩進みます.太郎くんと次郎くんの進む速さの比を求めなさい.
「同じ距離を進むのに要する歩数」と「同じ時間に進む歩数」という2種類の歩数が出てくることが,この問題をややこしくしています.
この二つの条件から道のりの比が7:6,時間の比が6:7として速さの比を求めようとするのは早計です.
太郎くんが7歩で進む距離を次郎くんは6歩で進むということは,ここから歩幅が求められます.
進む道のりを1mとすると,太郎くんと次郎くんの1歩の長さ(歩幅)はそれぞれ
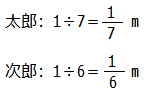
となります.
つぎに,太郎くんが6歩進む間に次郎くんは7歩進むことから,この時間に進む道のりがわかります.
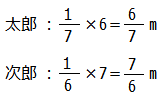
よって道のりの比は
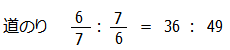
となります.
道のりの比が36:49,時間の比は1:1なので,速さの比は「道のり÷時間」で
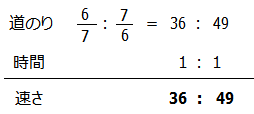
よって,求める速さの比は36:49となります.
単純な「道のり」「時間」「速さ」とは少し異なる「歩数」と「歩幅」ですが,具体的な量を決めることで問題がわかりやすくなります.
ここでは具体的に「道のりを1m」とおいて歩幅を計算していますが,この場合,7歩と6歩の最小公倍数で42mにしても構いません.その方が分数の計算がなくなるので分かりやすくなります.(ただし6歩や7歩で42mも進むというのは非現実的ではあります)
関連情報
