速さと比(時計算その２)

速さと比(時計算その１)では，時計算の基本的な計算方法を紹介しました．

今回は，時計算のよくある演習問題を紹介してみたいと思います．

まず，7時ちょうどのときの長針と短針の角度は，

30×7＝210°　です．

これが90°になるときを求めれば良いのですが，「2回目」というところに注意です．

想像してみてください．7時から8時までには7時20分くらいで一度90°になり，7時35分くらいで長針と短針が重なって，7時50分くらいで再び90°になりそうな気がしませんか？

重要なのは，長針と短針は一度「重なっている」という点です．つまり，長針は「210°の差を追いついた後，さらに90°引き離した」ことになります．

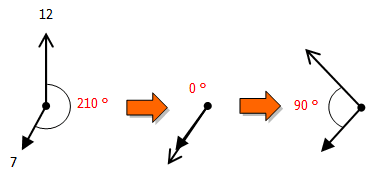
よって，計算式は次の通りとなります．

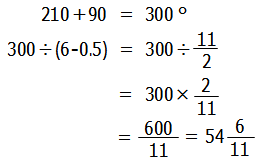
以上より，答えは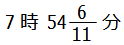，となります．

※ここでも，速さと比(時計算その１)で述べたように，問題を読んだ段階で「答えがだいたいどれくらいになるか」を判断する力が大切になってきます．

これは少し応用問題になります．

まず，10時ちょうどのときの長針と短針の角度(小さいほう)は，

360－30×10＝60°　です．

これが，左右対称になるのですから，図としては次のように描けます．

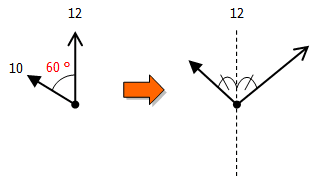
図より，大体10時10分前後であることが想像できると思います．

ここで，長針と短針の動きをもう少し詳しく見てみましょう．

10時ちょうどからの針の動きをたどると，次のように描けます．

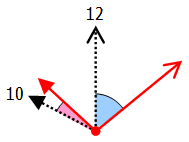
いま，12をはさんで左右の角度は等しいので，上の図で長針が動いた角度(水色の角度)は次のように反転させることができます．

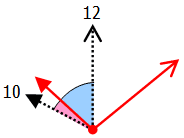
上の図から，図のピンク色の角度と水色の角度は合計すると60°になることがわかるはずです．

ということは，「求める時刻になるまでに長針と短針は合わせて60°動いた」ことになります．

よって，求める時刻は以下のように計算することができます．

※この計算では(6－0.5)ではなく，(6＋0.5)になることに注意です．

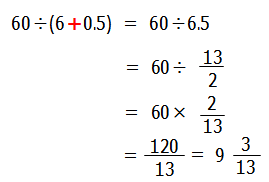
以上より，答えは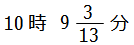，となります．

※時計算は(6－0.5)の計算しかしない，と思い込んでいると，このような問題でミスをしがちです．この問題では長針の動いた角度が左右反転しているので，いつものような追いつき算ではなく，出会い算になっています．

ちなみにこの問題は，次のように解くこともできます．

長針は毎分6°，短針は毎分0.5°動きますが，ここで新たに「長針と短針のちょうど真ん中を動く針」を考えてみます．

図で表わすと，次の赤い針が「真ん中の針」です．

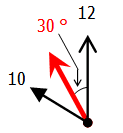
10時ちょうどのときの長針と短針の小さいほうの角度は60°なので，真ん中の針と長針の作る角度は30°になります．

そして，真ん中の針は左右対称の時刻になるときにちょうど12を指します．

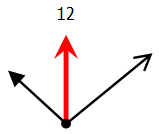
ということは，真ん中の針が求める時刻までに動いた角度は30°であることがわかります．

真ん中の針は毎分何度で動くのでしょうか？

長針は毎分6°，短針は毎分0.5°動きますから，真ん中の針は1分間に，

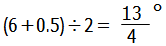　ずつ動きます．

よって求める時刻は以下のように計算することができます．

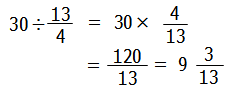
以上より，答えは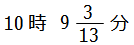，となります．

※初見の問題でいきなり「真ん中の針」を考えるのは非常に困難ですが，計算自体は先ほどよりもシンプルになります．「対称となる時刻」の問題だったら真ん中の針を考える，という手法を自分の頭の中の引き出しにあらかじめインプットしておくのもひとつの手です．