速さと比の演習(比の活用)

速さと比の分野では，「道のり」「時間」「速さ」の比を利用することが多々あります．ここでは比をうまく活用することが必要な問題に取り組んでみます．

さっそく次の問題を見てみましょう．

現実的に考えると100m走では加速する時間もあるので，スタートからゴールまで同じ速さで走りきることはありえません．しかし，加速を考慮すると高校の物理の範疇になってしまうので，こういった問題では常に「速さは一定」と考えます．

それはさておき，問題文から，同じ時間に進む道のりの比が計算できます．

太郎くんが100m走りきった時点で，次郎くんは100－20＝80m進んでいます．

よって，太郎くんと次郎くんの道のりの比は

100：80＝5：4

となります．

太郎くんのスタート地点を後ろにずらして2人が同時にゴールする，ということは次郎くんの走る道のりは100mだということです．

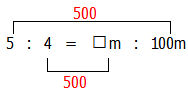
２人が同じ時間に進む道のりの比は5：4なので，太郎くんが走る道のりを□とすると，

太郎：次郎　＝　5：4　＝　□m：100m

と書けます．

外項の積＝内項の積なので

□＝5×100÷4＝125

と求められます．

問題は「何m後ろにすれば」なので，答えは

125－100＝25mとなります．

比を□を使って表わすときに太郎と次郎の「どちらを□とおくか」を間違えないように注意したいところです．

さて，これが次のような問題になるとどうでしょう？

問題の条件は問題1と同じです．じゃあ答えは「25m手前」じゃないの？と思うかもしれませんがそうはなりません．

ただ，問題の解き方そのものは問題1とまったく同じです．今回は次郎くんの走る道のりを□とするだけです．

よって

太郎：次郎　＝　5：4　＝　100m：□m

より，□＝80です．よって答えは100－80＝20mとなります．

なぜ，問題1と問題2では答えが違うのでしょうか？問題の条件が同じならば答えも同じになりそうですが・・・？

問題1と問題2の違いはどこにあるのでしょうか？？

そうです！問題1と2では「ゴールするまでにかかる時間が違う」のです．

太郎くんは問題1では125m，問題2では100m走っています．次郎くんは問題1では100m，問題2では80m走っています．両者とも問題1の方が走る距離が長くなっていますので，ゴールするまでにかかる時間は当然問題1の方が長くなります．２人の進む道のりの差は時間が長くなればなるほど大きくなるので，問題1の答えの方が問題2の答えより大きくなるのは当然のことなのです．

このように，問題1を解いた後に問題2を見たときに，「むむ，これは同じ答えにはならないな」という感覚を瞬時に持てるようになれば，かなり算数のセンスが磨かれてきたと言えると思います．