速さと比(旅人算の演習)

このページでは，旅人算としては比較的よく出題される『池の周囲を回る問題』の解法を確認したいと思います．

まずは基本問題です．

問題からは池の周囲の長さが分からないので，太郎と次郎の速さを計算することができません．

そんなときはどうするか・・・？　そうです！自分で勝手に決めてしまえばよいのです．

でも，勝手に決めるといっても何mにすればよいのでしょうか？

もうお気づきかもしれませんが，こういうときは最小公倍数にそろえるのが普通です．

太郎は20分，次郎は30分かかるのですから，池の周囲の長さは20と30の最小公倍数より，600mとおいてみましょう．

すると，太郎と次郎の速さはそれぞれ，

太郎：600÷20＝30m/分

次郎：600÷30＝20m/分

となります．

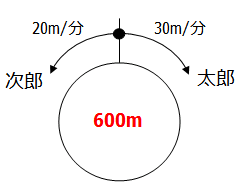
太郎と次郎が反対方向にまわるということは，出会い算になるわけですから，答えは，

600÷(30＋20)＝12分　と求まります．

では次の問題です．

この問題では池の周囲の長さを問われているので，問題１のように最初に池の周囲の長さを勝手に決める，という手順はナンセンスです．

この問題の場合，注目すべき点は「4分」という数値です．この4分間の動きに注目してみましょう．

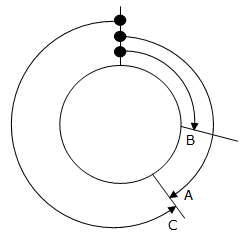
まず，AとCが出会ったときの様子を表わすと次のようになります．

その4分後にBとCが出会ったときの様子は次のようになります．

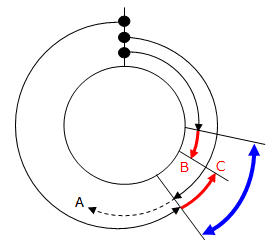
BとCの速さはわかっているので，この4分間でB,C2人の進んだ長さの合計は次のように計算することができます(上図の青の長さ)．

(60＋100)×4＝640m

ここで，もう一度AとCが出会ったときの様子に立ち返ってみましょう．

この640mというのは，AとCが出会ったときの，「AとBの進んだ距離の差」になっていることがわかるはずです．

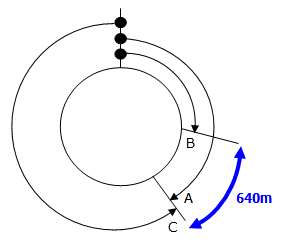
AとBの差は1分に80－60＝20mずつ開くのですから，640mの差ができるまでにかかった時間は，

640÷(80－60)＝32分　となります．

よって，AとCが出会ったのは出発してから32分後なので，池の周囲の長さは，

(80＋100)×32＝5760m　と求まります．

池の周囲をグルグル回る問題は旅人算の中では結構典型的な問題のひとつです．問題１程度の問題なら式だけで解けますが，問題２のように3人が別方向に動くときなどは，今回紹介したように図に描いてみる方がよいでしょう．

なお，今回使った図は説明のための簡便なものであり，図の描き方が線分図や面積図のように決まっているわけではありませんので，理解しやすいように適宜加工していただいたらよいかと思います．