逆算の考え方
四則混合計算の考え方については「四則混合計算」で詳しく解説していますが,同じ計算問題でもまちがいやすいのが,式中の□の値を求める逆算です.入試では普通の計算問題と同様に逆算の出題率も非常に高いので,計算まちがいをしないよう確実に解答したいところです.
逆算をするときにも通常の計算と同じようにまずは①,②,③・・・と計算の順番をつけます.
そして逆算のときに注意したいポイントは次の3点です.
- 通常の計算は①→②→③→だが,逆算では→③→②→①の順で計算する
- 番号をつけた記号(+-×÷)と逆の計算をする.ただし『-□』のときは引き算,『÷□』のときは割り算をする
- 計算できるところは先に計算してしまう.計算できないところは大きな□で置き換える
具体的な例を見ながら考えてみましょう.
この計算に順番をつけると次のようになります.

通常の計算は①→②の順で計算しますが,逆算の場合はそれを逆から順に②→①と計算してゆきますのでまず②の計算から実行します.その際計算できない部分は大きな□に置き換えてしまい,

と考えます.②の番号は掛け算(×)に対してつけられているので逆算は割り算になります.
つまり②の計算は『9÷3=3』となります.
この結果を用いて次に①の逆算を実行します.①の計算は,
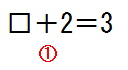
となります.①の番号は足し算(+)に対してつけられているので逆算は引き算になります.
つまり①の計算は『3-2=1』となり,答えは『1』となるのです.
分からなくなったら簡単な例で置き換えてみる
逆算の計算は,番号をつけた記号と逆の計算をします.『□+1=3』なら『□=3-1=2』です.『3×□=18』なら『□=18÷3=6』となります.
ただし,『-□』と『÷□』のときは逆にはなりません.例えば『5-□=2』の場合は『□=5-2=3』となります.『24÷□=6』なら『□=24÷6=4』となります.
このあたりの計算はどうしてもまちがいがちです.そのような時は簡単な例で考えるのがよいでしょう.
例えば問題が「345÷□=115」といった場合に,□を求めるには掛け算をしたらよいのか割り算をしたらよいのか分からなくなる,ということがあります.そんなときは簡単な九九の計算をあてはめて考えると分かりやすくなります.式として同じ形になるように例えば「6÷□=3」という問題を考えさせます.この問題ならおそらくどの子も「2」と即答してくれるはずです.そこで次になぜ答えが「2」になるかを考えさせます.登場する数字は6と3しかないわけですから6を3で割って答えが「2」になっていることが理解できるはずです.
ここまで分かればあとは同じように計算するだけです.「345÷□=115」は式の形として「6÷□=3」と同じなのですから,計算として「345÷115」をやればよいということが分かるのです.
計算できるところは先に計算する
例えば『□÷(4+2×3)=3』という問題の場合,よく見ると先に計算できる部分があるのが分かります.□の計算とは関係なくカッコの中は計算できてしまいます.このような先に計算できる部分は計算の順番をつける前に先に計算してしまいましょう.先に計算できるところを計算してしまうことでこの問題は『□÷10=3』という形に単純化できるからです.
以上のことをふまえて次のような問題を考えてみましょう.
まずこの問題では2×3-1が先に計算できるのでその分を先に計算してしまいます.2×3-1=5なので,この問題は5+[{20÷(□-5)+7}-2]=15と書くことができます.少しだけ単純になりましたね.
次に計算の順番を書き込みます.

逆算なので⑤から順に計算してゆきます.⑤の計算は計算できないところを大きな□とすると,

と書くことができます.
⑤の計算は□=15-5=10となります.
次に④の計算です.④の計算は,

となるので,□=10+2=12となります.
次に③の計算は,

となるので,□=12-7=5となります.大きな□がだいぶ小さくなってきました.
次に②の計算は,

となるので,□=20÷5=4となります.(←計算注意!)
最後に①の計算です.
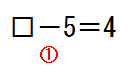
この計算は□=4+5=9となり,求めたかった□は『9』であることが分かりました.
いかがでしょうか?通常の計算よりちょっと複雑でまちがいやすい逆算ですが,計算の順番を正しく把握すること,どんな計算をしたらよいか分からなくなったら簡単な例をあてはめてみること,などを心掛ければ確実に答えに辿りつけるはずです.
