過不足算の演習２

過不足算の線分図の描き方には慣れてきたでしょうか？ここでは過不足算の考え方を再確認する意味でも有益と思われる問題の演習に取り組んでみましょう

さっそく線分図を描いてみたいところですが，この問題では配り方のパターンが多いので，このままでは少し分かりにくいです．

ですので，ちょっと整理してみましょう．

生徒全員に6本ずつ配ると453本不足することが分かっているので，同じく生徒全員に●本ずつ配ると●●本余る/不足する，ということがわかれば線分図を描くことができます．問題を読むと各学年に違う数ずつ配っていますが，これを同じ数ずつ配ることを考えてみましょう．

同じ数ずつ配る・・・さてそれは何本にしたらよいでしょうか？問題を読むと，それはおそらく「3本」か「4本」か「5本」であることは想像できると思います．いま，1年生と2年生の人数はわかっていますが3年生の人数はわかりません．ということは・・・

そうです！この場合は人数がわかっていない“残りの生徒”の「5本」にそろえるのが正解です．

というわけでさっそく全学年に5本ずつ配ることにしてみましょう．

1年生は88人に3本ずつ配るのをやめて5本ずつ配ることにすると，1人あたり2本ずつ不足することになります．

ということは，2×88＝176本不足することになります．

2年生は86人に4本ずつ配るのをやめて5本ずつ配ることにすると，1人あたり1本ずつ不足することになります．

ということは，1×86＝86本不足することになります．

残りの生徒には5本ずつ配っているので過不足は発生しません．

配る本数を5本にそろえた理由がここにあります．仮に5本以外の本数にそろえようとすると「残りの人数」が何人かわからないので，過不足の本数が求められないのです．

さて，5本にそろえると1年生では176本不足，2年生は86本不足，残りの生徒は過不足なしとなります．つまり，全学年では176＋86＝262本不足となります．ここまでわかればさっそく線分図を・・・といきたいところですが，早まってはいけません．

というのも最初の状態では「77本余っている」ことを忘れているからです．77本余っているところから262本足りなくなるので，実際の不足本数は，262－77＝185本となります．

というわけで，この問題は「生徒全員に6本ずつ配ると453本不足し，5本ずつ配ると185本不足する」という普通の過不足算になりました．ここまでできたらあとは線分図を描いて計算するだけです．

まずはお約束どおり，はじめに鉛筆の長さを先に決めておきます．

生徒全員の人数を①として，過不足の状態を線分図にすると次の通りです．

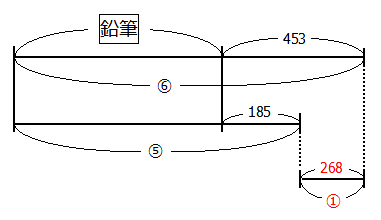
線分図の差をとることにより，①＝453－185＝268，つまり生徒全員の人数は268人と求めることができます．

この問題では，過不足を「そろえる」という操作が必要となります．「何本にそろえたらよいか」が重要なのもさることながら，そもそも過不足算の基本をよく理解していないと「そろえ方」がわからなくなります．そういった意味で，「過不足算を正しく理解しているか」を確認するためにもこの問題は効果的かと思います．