和差算の基本

和差算とは二つ以上の数の和や差が分かっているときにそれぞれの数を求める，という問題です．文章題としては基本事項であり，純粋に和差算単独で出題される場合も多いですが，問題を解いてゆく過程の一部で和差算の考え方を利用する，という場合もあります．今回はそんな和差算の基本的な考え方を確認しておきましょう．

では具体的な問題を見てみましょう．

問題を読むと，今どき「おはじき」って・・・と突っ込みたくなりますが，算数の問題では意外とおはじきは人気があります．（「碁石」や「玉」も人気があります．いつも思いますが「玉」ってなんなんだろう…??）ついでに，人物名では太郎くん，花子さん，あきらくん，などが人気です．「ウィリアムくんが碁石を…」みたいな問題は見たことがありません．（たまに「学校名」がついた人物が登場することはあります）．

それはさておき，和差算は基本的に線分図で考えます．まずは問題文の状態を線分図にしてみましょう．

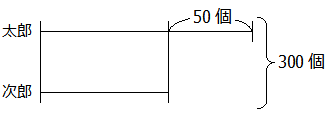
線分図から，合計の300個から50個を引くと二人の持っているおはじきの数は等しくなることがわかります．

つまり，
(300-50)÷2＝125
の計算をすることで次郎くんのおはじきの数が125個と求まります．

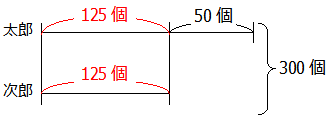
太郎くんのおはじきは次郎くんより50個多いのですから
125＋50＝175個

となります．

以上の流れではまず「次郎くんのおはじきの数」を先に求めましたが，先に太郎くんのおはじきの数を求めることもできます．

この場合，線分図は『太郎くんにそろえるように』描きます．

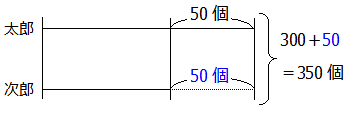
線分図を太郎くんにそろえると，合計の数は300＋50＝350個になります．

よって，350÷2＝175と計算することで太郎くんのおはじきは175個と求めることができます．（次郎くんのおはじきの数は175－50＝125個）

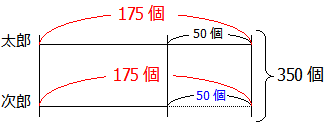
以上二つのうちどちらの線分図で考えるかは問題によります．この問題のように『二人の』おはじきの数を求めるときはどちらでも良いですが，問題が『太郎くんのおはじきの数を求めなさい』であれば，太郎くんにそろえる線分図で，『次郎くんのおはじきの数を求めなさい』であれば，次郎くんにそろえる線分図で考えた方が計算時間の短縮になります．

算数にはＡ，Ｂ，Ｃなどの味気ない人物もよく登場します．そして「ひもを分ける」というまったくもって目的がよく分からない問題も多数出題されます．

それはさておき，この問題もまず線分図に表してみましょう．この問題の場合は和や差は分からない代わりに『比』がわかっています．ＡもＣもＢを基準として２倍，５倍となっているのでここでは『Ｂを①と置く』ことが重要です．このことをふまえて線分図を描くと次のようになります．（このとき６mはちゃんと600cmにしておきましょう．単位換算に不安があれば→こちら）

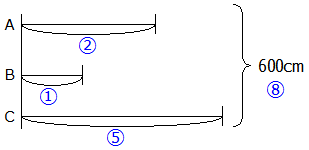
ここでポイントとして①や②などの比を表す数は基本的に線分図の下に，ＯＯ個，ＯＯcmなどの具体的な数は線分図の上に書くようにするとわかりやすいでしょう．（あくまでも”基本的に”です．線分図が複雑になったり，そもそも比しか登場しない問題などはこの限りではありません）

線分図より，600cmは②＋①＋⑤＝⑧にあたることがわかります．

⑧＝600cm

　　↓

①＝600÷８＝75cm

であるので，

②＝75×２＝150cm

⑤＝75×５＝375cm

となり，Ａ，Ｂ，Ｃがそれぞれもらうひもの長さは，Ａ：150cm，Ｂ：75cm，Ｃ：375cmと求まります．

文章題では，和差算に限らず『問題文の状態を図に表す』ことが重要です．ここで言う『図』とは線分図や面積図です．図に表すということは問題が視覚的にわかりやすくなるばかりでなく，問題の文章を読むだけでは気付かない“解答の流れ”を見つけ出すきっかけにもなります．
線分図の描き方には人それぞれ癖があります．線分図を分割して線を降ろすときに実線で描くか点線で描くか，など細かいところは人それぞれでしょう．しかし，基本的な考え方は同じなはずですから自分が最も理解しやすいような形で線分図を多用できるようになりましょう．