消去算の基本

消去算とは一方の数に揃えて引き算することでもう片方の値を求めるという問題です．文章で書くとなんだかあいまいにしか表現できませんが，問題を解いてみるとその意味はすぐにわかります．

では具体的な問題を見てみましょう．

この問題は「Ａ，Ｂどちらかに揃えて消す」ことで値段を求めることができます．ではＡ，Ｂどちらに揃えればよいでしょうか？

もちろんどちらを消しても答えは求まりますが，消去算の基本は「答えを求めなくてもよい方に揃える」ことです．ですのでこの問題の場合は『Ｂ』に揃えて消せばよいことになります．

さて，では具体的な解法を見てみましょう．

問題を読んだだけではＡもＢも値段がわかりません．ですので，Ａ１冊の値段を①，Ｂ１冊の値段を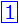と置いてみましょう．

すると，問題の様子は次のように表すことができます．

この式から「□を消す」にはどうすればよいでしょうか？

そうです．毎度おなじみ「最小公倍数」に揃えてしまえばよいのです．３と５の最小公倍数は15です．15に揃えるには，２つの式はそれぞれ５倍，３倍すればよいので，次のように変形できます．

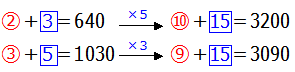
この二つの式を引き算すると，

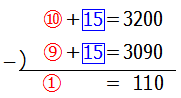
となります．最初にＡ１冊の値段を①と置いたのですから，答えは110円となります．

消去算では上の解法の他に，

Ａ×２＋Ｂ×３＝640

Ａ×３＋Ｂ×５＝1030

と書いて解く方法もあります（書き方の違いだけで考え方そのものは同じです）．ただしこの式は消去算でしか利用できないのに対し，①と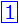を使う方法は他の分野の問題でも多用するのでここでは①と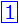を使った方法で解説しています．

まずは鉛筆１本の値段を①，消しゴム１個の値段を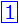とおいてみましょう．
すると，問題の様子は次のように書けます．

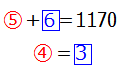
この問題では「消しゴム」すなわち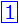を求めたいのですから，○を消せばよいことになります．５と４の最小公倍数は20ですので上の式は次のように変形できます．

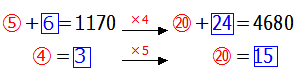
よって，

となるので，

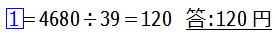
と求めることができます．

上の解説では基本に沿って鉛筆に揃えて消しましたが，この問題では消しゴムに揃えるほうが計算が簡単です（６と３の最小公倍数は６なので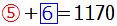の式は変形する必要がない）．

ですので，慣れてくれば敢えて消しゴムに揃えて解く，というのもアリです．

このように「どちらに揃えればよいか」だけでなく「どちらに揃えれば計算が楽か」を考えることも重要です．

りんご１個の値段を①みかん1個の値段を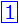と置いてみましょう．

すると問題の様子は，

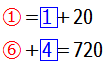
このようになります．この問題はりんごもみかんも求めなくてはいけないので○と□のどちらに揃えて解いてもよいです(※)．ここではとりあえず○に揃えて解いてみましょう．

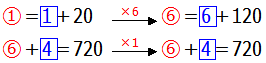
このように変形できるので，

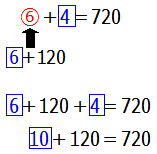
と計算できます．よって，

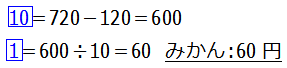
と求めることができます．りんご１個はみかん１個より20円高いので，

60＋20＝80　　りんご：80円

と求まります．

(※)上の解法では，さりげなく○に揃えて解いていますが，これを□に揃えて解くことももちろん可能です．

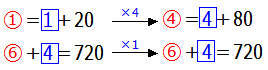
と書けますが，ここで次のような式の変形が必要となります．

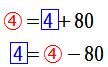
この式の変形は四則混合計算の□を求める逆算と同じですが，小学生にはややわかりにくい計算です．

ですので，「○と□のどちらに揃えて解いてもよい」とは言うものの，この場合は○に揃える方が賢明です．

問題2でも述べましたが，「どちらに揃えれば計算が楽か」を判断する力がここでも求められるというわけです．