植木算の演習

植木算の基本では，植木算の基本次項を確認しましたが，植木算というのは，他の分野の問題に隠れていることの方が圧倒的に多いかと思います．

ここでは，そのような植木算が隠れている問題や，植木算の発展事項を確認したいと思います．

では問題を見てみましょう．

仕事算の基本でも解説していますが，この場合は1人が1日でできる仕事を①としてみましょう．

すると，全体の仕事は，①×10人×21日＝となります．

これを9人で終わらせたのですから，もし1日も休まずに働いたとしたら，

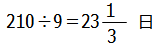　で終わることになります．

ここで注意したいのは，日数が分数になってしまったという点です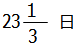．で終わったということは，23日目では仕事は終わっておらず，24日目にいつもの1/3だけ働いたら仕事が終わったということです．

つまり，9人が休まずに働けば24日目に仕事が終わるのですが，次に考えなくてはならないのが「休日」です．

3日仕事をしたあとに1日の休日が発生するので，これを図に表すと次のようになります．

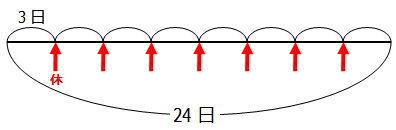
図より，休日の数は，24÷3＝8　8－1＝7日　となります．

※通常の植木算なら，24÷3＝8　8＋1＝9日と計算したいところですが，この問題の場合，「初日」と「最終日」の2日は休日にはならないので，実際の休日の数は9日より2日少ない7日となります．

休日の数が7日とわかったので，求める答えは，

24＋7＝31日目となります．

このように，植木算の応用問題は『植木算的要素が隠れている問題』とも言えます．そして，上の問題の場合では植木算の基本がそのままでは通じない，という応用問題にもなっています．

『植木算的要素』があれば，計算だけで解決しようとせず，簡単な図を描いて確認してみるのが一番です．

さて，次は植木算そのものの発展形を考えてみたいと思います．

植木算の基本で紹介した問題は，言い換えてみれば「線を点で分ける」問題です（道路が『線』，木が『点』にあたります）．

これを発展させると「面を線で分ける」問題というのも考えられます．

例えば次のような問題です．

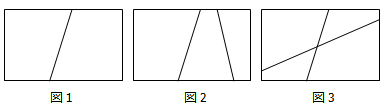
これはかなり応用問題です．問題を読んだだけで，これが「植木算の発展形」だと気付ける小学生はほぼ皆無かと思われます．

問題の図には2本引いたときまでしか描かれていないので，とりあえず線を3本引いたときを考えてみましょう．

「最も多くの部分に分けるように」3本目の線を引くということは，すでに引かれている2本の線の両方に交わるような線を引けばよいことになります．

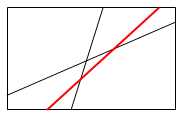
上図のように線を引くと，7個の部分に分けられることがわかります．

ここまでのことを一度表にまとめてみましょう．「線の本数」と「分けられる部分の数」の関係は次の通りです．

分けられる部分の数について，気付くことはないでしょうか？　そうです！これは階差数列が等差数列になっている数列です．

※階差数列を利用する場合の□番目の数の求め方については「階差数列の利用」を参考にしてください．

表より，この問題は『1,2,4,7・・・と続く数列の11番目の数』を求めよ，という問題に置き換えられます(「線の本数」は0から始まっているので，線の本数が10のときは数列としては11番目になります)．

この数列の差をとってみると，次のようになります．

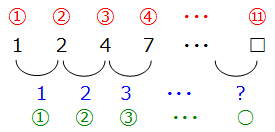
ここで，植木算の基本に立ち返ると，数字が11個あるときは，あいだの数は10個になりますから，階差数列の「？」は10番目の数になります．さらに，階差数列は「1,2,3,・・・」と続いていますから10番目は「10」になります．

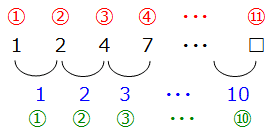
求める数は，数列の初項に階差数列を足せば求まります．

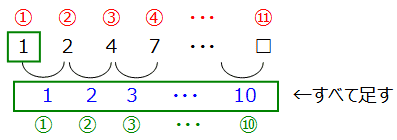
これを式に表わすと，1＋(1＋2＋3＋・・・＋10)となります．

1から10までの和は，(1＋10)×10÷2＝55　ですので，

1＋(1＋2＋3＋・・・＋10)＝1＋55＝56個　が求める答えとなります．

(※1から10までの和＝55というのは覚えておいてもよいと思います)

線を点で分ける問題に比べ，面を線で分ける問題は格段に難しくなります．これをさらに発展させると「立体を面で分ける」問題というのも考えられます．植木算の応用問題というのは，普通は今回紹介した問題１のような「問題中に植木算が潜んでいる」ものになりますが，植木算そのものも，実はものすごく発展的な考え方ができる概念でもあったのです．